Question

How do you find the equation of the ellipse with foci $\left( \pm 5,0 \right)$ and major axis of length 12.

Answer 1

In this problem, we are asked to find the equation of the ellipse, where the point of foci and the length of the major axis are given. Through the given major axis we can find the value of a and from the foci point we can find the value of b and the centre point, which is the origin here. Substituting these values we can get the equation of the ellipse.

Complete step by step answer:

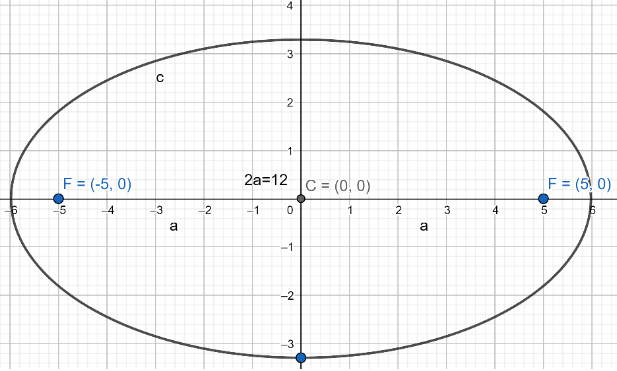
We know that the standard cartesian form of the equation of the ellipse is
$\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$, a>b ….... (1)
Here h and k are the centre and a is half length of the major axis and b is half length of the major axis.
We know that the given point of foci is $\left( \pm 5,0 \right)$which is of the general form $\left( \pm c,0 \right)$for horizontal ellipse.
$\Rightarrow c=5$……. (2)
From the given point of foci, we came to know that the centre point is $\left( 0,0 \right)$
Now we can write the equation (1) as

& \dfrac{{{\left( x-0 \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-0 \right)}^{2}}}{{{b}^{2}}}=1 \\\ & \Rightarrow \dfrac{{{\left( x \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y \right)}^{2}}}{{{b}^{2}}}=1......(3) \\\ \end{aligned}$$ Now we have to find the value of a and b, to get the equation of ellipse. We know that the length of the major axis is 2a. We also know that the given length of the major axis = 12. Now we can substitute the length of the major axis to the given length, we get $$\begin{aligned} & \Rightarrow 2a=12 \\\ & \Rightarrow a=\dfrac{12}{2} \\\ & \Rightarrow a=6 \\\ \end{aligned}$$ Now we have to find the value of b. We know that the formula to find focus is $$\begin{aligned} & {{c}^{2}}={{a}^{2}}-{{b}^{2}} \\\ & \\\ \end{aligned}$$ We already know the value of c from (2) As we know the focus point and the value of a, we can find the value of b $$\begin{aligned} & {{5}^{2}}={{6}^{2}}-{{b}^{2}} \\\ &\Rightarrow b=\sqrt{{{6}^{2}}-{{5}^{2}}} \\\ &\Rightarrow b=\sqrt{36-25} \\\ &\Rightarrow b=\sqrt{11} \\\ \end{aligned}$$ Now we got the value of a and b, we can substitute it in the equation (3), we get $$\begin{aligned} & \Rightarrow \dfrac{{{\left( x \right)}^{2}}}{{{6}^{2}}}+\dfrac{{{\left( y \right)}^{2}}}{{{\left( \sqrt{11} \right)}^{2}}}=1 \\\ & \Rightarrow \dfrac{{{x}^{2}}}{36}+\dfrac{{{y}^{2}}}{11}=1 \\\ \end{aligned}$$ **Therefore, the equation of the ellipse is $$\dfrac{{{x}^{2}}}{36}+\dfrac{{{y}^{2}}}{11}=1$$.** **Note:** In these types of problems, it is necessary to check for the centre point, in this problem it is the origin, if the centre point is not the origin, we will get a different solution. Students make mistakes in writing the incorrect formula. It can be rectified by practising these types of problems.