Question
Question: How do you find the equation of an ellipse with foci \(\left( { \pm 2,0} \right)\) and major axis of...
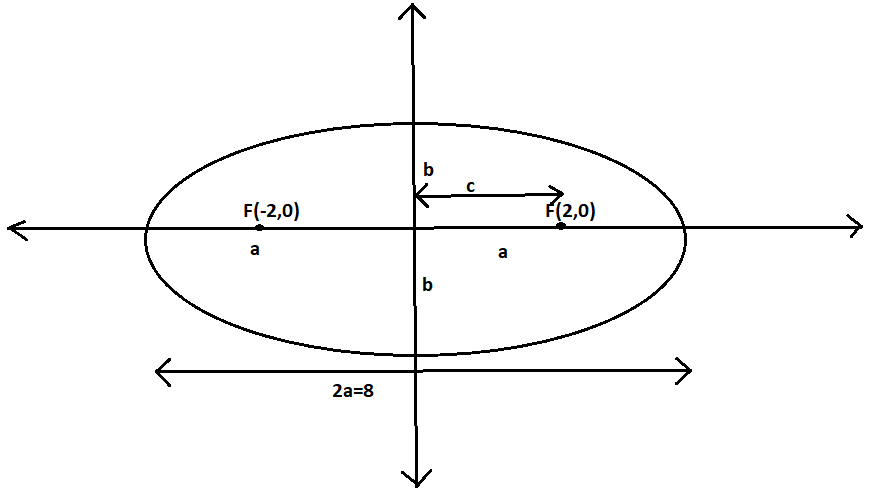
How do you find the equation of an ellipse with foci (±2,0) and major axis of length 8 ?
Solution
In this problem, we are asked to find the equation of the ellipse, where the point of foci and the length of the major axis are given. Through the given major axis, we can find the value of a and from the foci point we can find the value of b and the centre point, which is the origin here. Substituting these values, we can get the equation of the ellipse.
Complete solution:
We know that the standard cartesian form of the equation of the ellipse is
⇒a2(x−h)2+b2(y−k)2=1a>b−−−−(1)
Here h and k are the centre and a is half length of the major axis and b is half length of the minor axis. We know that the given point of foci is (±2,0)
which is of the general form$$$$$$( \pm c,0)forhorizontalellipses. \Rightarrow c = 2 - - - \left( 2 \right)Fromthegivenpointoffoci,wecametoknowthatthecentrepointis\left( {0,0} \right)Nowwecanwritetheequation\left( 1 \right)as\dfrac{{{{(x - 0)}^2}}}{{{a^2}}} + \dfrac{{{{(y - 0)}^2}}}{{{b^2}}} = 1 \Rightarrow \dfrac{{{{\left( x \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( y \right)}^2}}}{{{b^2}}} = 1......(3)Nowwehavetofindthevalueofaandb,togettheequationofellipse.Weknowthatthelengthofthemajoraxisis2a.Wealsoknowthatthegivenlengthofthemajoraxis = {\text{ 8}}.Nowwecansubstitutethelengthofthemajoraxistothegivenlength,weget \Rightarrow 2a = 8 \Rightarrow a = \dfrac{8}{2} \Rightarrow a = 4Nowwehavetofindthevalueofb.Weknowthattheformulatofindfocusis{c^2} = {a^2} - {b^2}Wealreadyknowthevalueofcfrom\left( 2 \right)Asweknowthefocuspointandthevalueofa,wecanfindthevalueofb{2^2} = {4^2} - {b^2} \Rightarrow {b^2} = {4^2} - {2^2} \Rightarrow b = \sqrt {{4^2} - {2^2}} \Rightarrow b = \sqrt {16 - 4} \Rightarrow b = \sqrt {12} Nowwegotthevalueofaandb,wecansubstituteitintheequation(3),weget \Rightarrow \dfrac{{{{(x)}^2}}}{{{{\left( 4 \right)}^2}}} + \dfrac{{{{(y)}^2}}}{{{{\left( {\sqrt {12} } \right)}^2}}} = 1 \Rightarrow \dfrac{{{{(x)}^2}}}{{16}} + \dfrac{{{{(y)}^2}}}{{12}} = 1$$
Therefore, the equation of the ellipse is16(x)2+12(y)2=1
Note:
In these types of problems, it is necessary to check for the centre point, in this problem it is the origin, if the centre point is not the origin, we will get a different solution. Students make mistakes by takes major axis as 2b instead of 2a.
