Question

How do you find the equation of a parabola with vertex at the origin and focus $\left( 0,-2 \right)$

Answer 1

Here in this question we have been asked to find the equation of a parabola with vertex at the origin and focus $\left( 0,-2 \right)$ . We know that the general form of parabola is given as ${{x}^{2}}=4ay$ has a vertex $\left( 0,0 \right)$ and focus at $\left( 0,a \right)$.

Complete step by step solution:
Now considering from the question we have been asked to find the equation of a parabola with vertex at the origin and focus $\left( 0,-2 \right)$ .
From the basics of concept we know that the general form of parabola is given as ${{x}^{2}}=4ay$ has a vertex $\left( 0,0 \right)$ and focus at $\left( 0,a \right)$ .
If we observe the given information carefully then we can say that $a=-2$ .
Therefore we can conclude that the equation of a parabola with vertex at the origin and focus $\left( 0,-2 \right)$ is given as ${{x}^{2}}=-8y$ .

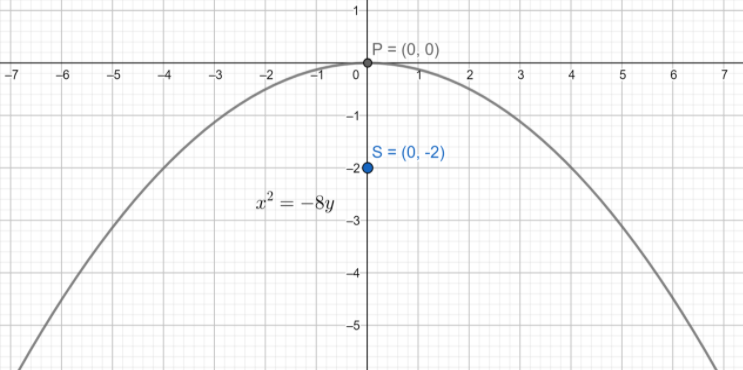
Here we can see the graph of the required parabola for a reference.

Note: While answering this question we should be sure with our concept mainly because if we are aware of basics then it looks very simple and we can solve it within a short span of time. Very few mistakes are possible in this question. Similarly we can find the equation of any parabola. For example if we have a parabola with vertex $\left( 0,0 \right)$ and focus $\left( 0,2 \right)$then the equation is given as ${{x}^{2}}=8y$ .