Question

How do you find the equation of a circle with radius 6 and center (2,4)?

Answer 1

This is a question of 2D geometry. To find the equation of a circle with center and radius given we need to find the locus of a point which has a fixed distance as radius from the center point. We will be using the distance formula given by $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$.

Complete step by step answer:
Here we are given the center as (2,4) and radius of the circle as 6 units. We will use the distance between points formula to find the locus of the point that is the circle.
The distance between two points in 2D , $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given by the distance formula as
\Rightarrow $$$$\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}
In the case of a circle this distance is fixed and called Radius (r) . So the equation can be given as
\Rightarrow $$$$\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}=r
Squaring both side we get
\Rightarrow $$$${{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}={{r}^{2}}.......(1)
In the above question we are given the fixed radius r that is 6 units and center (2,4).
Now we assume a point on the circle say (x,y)
Then in equation (1) we substitute the values $\left( {{x}_{1}},{{y}_{1}} \right)$as (2,4) and $\left( {{x}_{2}},{{y}_{2}} \right)$ as (x,y) and r as 6.
Now we get
\Rightarrow $$$${{\left( {{x}_{{}}}-{{2}_{{}}} \right)}^{2}}+{{\left( {{y}_{{}}}-4 \right)}^{2}}={{6}^{2}}

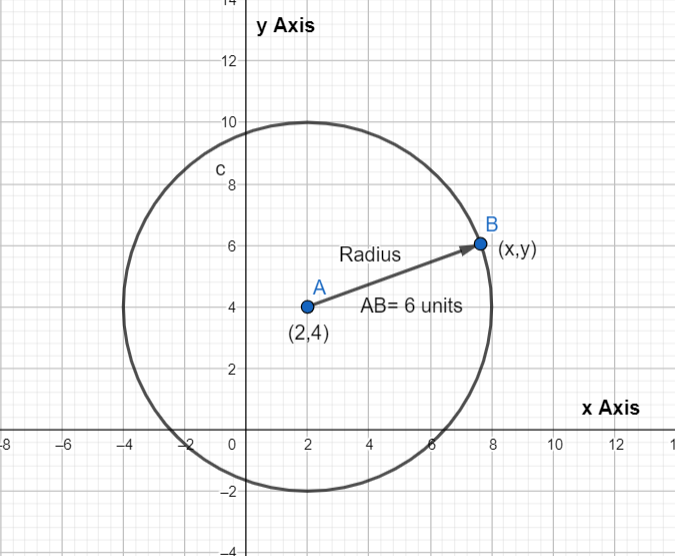
Thus the required equation of circle with center (2,4) and radius 6 is given by
\Rightarrow $$$${{\left( {{x}_{{}}}-{{2}_{{}}} \right)}^{2}}+{{\left( {{y}_{{}}}-4 \right)}^{2}}={{6}^{2}}

Note:
The required equation can also be calculated by comparing the given terms to the general form of equation of circle that is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c$ where the center of circle is given by
(-g.-f) and radius is given as $r=\sqrt{{{g}^{2}}+{{f}^{2}}-{{c}^{2}}}$.
Calculating the values of g, f and c and substituting back to the general equation we can get the required equation of the circle.