Solveeit Logo
Login

Question

Question: How do you find the equation of a circle whose center lies on the line \(2x+y-1=0\) and which passes...

How do you find the equation of a circle whose center lies on the line 2x+y−1=02x+y-1=0 and which passes through the point A(−2,0)A\left( -2,0 \right) and B(5,1)B\left( 5,1 \right)?

Explanation

Solution

In this question we have been given that the center of a circle lies on the line 2x+y−1=02x+y-1=0. We know the general equation of a circle is (x−h)2+(y−k)2=r2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}. Since the center passes through the given points A(−2,0)A\left( -2,0 \right) and B(5,1)B\left( 5,1 \right), we will substitute these values in the equation and equate both the equations to find the value of hh and kk, which are the coordinates for the center of the circle and then find the radius rr using the equation and then write the final equation of the circle.

Complete step-by-step solution:
We know that the standard form of the equation of a circle is (x−h)2+(y−k)2=r2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}, where (x,y)\left( x,y \right) is any point on the circle and (h,k)\left( h,k \right) is the center of the circle and rr is the radius of the circle.
Now we know that the circle passes through points A(−2,0)A\left( -2,0 \right) and B(5,1)B\left( 5,1 \right).
On substituting them in the general form, we get:
⇒(−2−h)2+(0−k)2=r2\Rightarrow {{\left( -2-h \right)}^{2}}+{{\left( 0-k \right)}^{2}}={{r}^{2}}
⇒(5−h)2+(1−k)2=r2\Rightarrow {{\left( 5-h \right)}^{2}}+{{\left( 1-k \right)}^{2}}={{r}^{2}}
Since there is r2{{r}^{2}} in the right-hand side in both the equations.
On equating, we get:
⇒(−2−h)2+(0−k)2=(5−h)2+(1−k)2\Rightarrow {{\left( -2-h \right)}^{2}}+{{\left( 0-k \right)}^{2}}={{\left( 5-h \right)}^{2}}+{{\left( 1-k \right)}^{2}}
On expanding the terms using the formula (a−b)2{{\left( a-b \right)}^{2}}, we get:
⇒4+4h+h2+k2=25−10h+h2+1−2k+k2\Rightarrow 4+4h+{{h}^{2}}+{{k}^{2}}=25-10h+{{h}^{2}}+1-2k+{{k}^{2}}
On combining the like terms, we get:
⇒4+4h=25−10h+1−2k\Rightarrow 4+4h=25-10h+1-2k
On rearranging the terms and simplifying, we get:
⇒2k=−14h+22\Rightarrow 2k=-14h+22
On dividing both the sides by 22, we get:
⇒k=−7h+11→(1)\Rightarrow k=-7h+11\to \left( 1 \right)
Now the equation of the line given is 2x+y−1=02x+y-1=0, on center point it becomes:
⇒2h+k−1=0\Rightarrow 2h+k-1=0
On writing it in the slope intercept form, we get:
k=−2h+1→(2)k=-2h+1\to \left( 2 \right)
Now on doing (1)−(2)\left( 1 \right)-\left( 2 \right), we get:
⇒k−k=−7h+2h+11−1\Rightarrow k-k=-7h+2h+11-1
On simplifying, we get:
⇒0=−5h+10\Rightarrow 0=-5h+10
On rearranging and simplifying, we get:
⇒h=2\Rightarrow h=2
Now on substituting h=2h=2 in equation (2)\left( 2 \right), we get:
k=−2(2)+1k=-2\left( 2 \right)+1
On simplifying, we get:
k=−3k=-3
Therefore, the standard form of the circle becomes:
(−2−2)2+(0−(−3))2=r2{{\left( -2-2 \right)}^{2}}+{{\left( 0-\left( -3 \right) \right)}^{2}}={{r}^{2}}
On simplifying, we get:
(−4)2+32=r2{{\left( -4 \right)}^{2}}+{{3}^{2}}={{r}^{2}}
On rearranging and taking the square root, we get:
r=5r=5.
On substituting the center and radius of the circle in the standard form, we get:
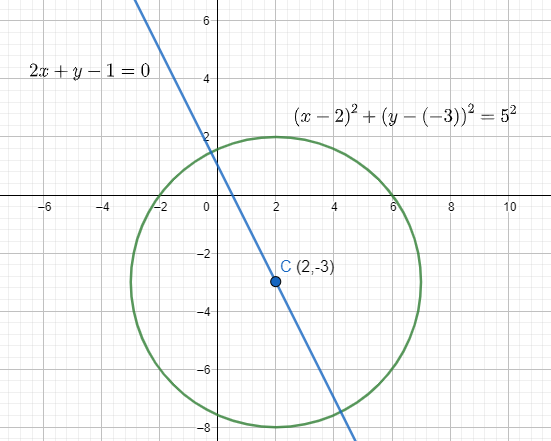
(x−2)2+(y−(−3))2=52{{\left( x-2 \right)}^{2}}+{{\left( y-\left( -3 \right) \right)}^{2}}={{5}^{2}}, which is the required solution.
On drawing the circle and the line on the graph, we get:

Note: In this question the main objective is that a point on a circle is equidistant from the center of the circle. When we took the square root of the term, only the positive value of the term was considered because distance cannot be negative therefore, it has to be discarded. The general formula of a circle with its center at the origin is given by the formula x2+y2=r2{{x}^{2}}+{{y}^{2}}={{r}^{2}}.