Question

How do you find the equation for a line with slope 5 and y intercept $-4$ ?

Answer 1

Hint : We first take the general equation of a line where we have the slope and y intercept form as $y=mx+c$ . We put the given values of slope $m=5$ and y intercept $-4$ . Then we place the equation in the graph to visualise its intercept form. We can see that the graph passes through $\left( 0,0 \right)$ .

Complete step-by-step answer :
We take the general equation of the line with the slope $m$ as $y=mx+c$ .
It’s given that the value of the slope for our required line is 5.
Putting the value in the equation of $y=mx+c$ , we get $y=5x+c$ .
As the y intercept $-4$ . That’s why the line passes through $\left( 0,-4 \right)$ .
Putting the value in the equation $y=5x+c$ , we get $-4=5\times 0+c$ .
This gives $c=-4$ .
The final equation of the line becomes $y=5x-4$ .

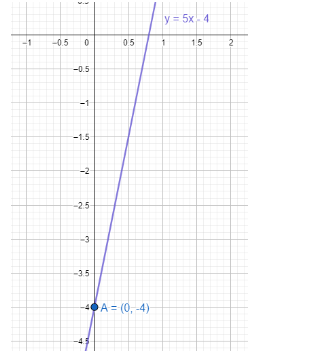
Note : For this equation $y=5x-4$ we can convert it into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$ . From the form we get that the x intercept, and y intercept of the line will be p and q respectively.
The given equation is $y=5x-4$ . Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$ , we get

& y=5x-4 \\\ & \Rightarrow 5x-y=4 \\\ & \Rightarrow \dfrac{5x}{4}+\dfrac{y}{-4}=1 \\\ & \Rightarrow \dfrac{x}{{}^{4}/{}_{5}}+\dfrac{y}{-4}=1 \\\ \end{aligned}$$ The form is determinate which gives that the intercept value is $ -4 $ and it passes through $ \left( 0,-4 \right) $ .