Question

How do you find the end behaviour and state the possible number of x intercepts and the value of the y intercept given $y={{x}^{2}}-4$?

Answer 1

We equate the given equation of parabolic curve with the general equation of ${{\left( x-\alpha \right)}^{2}}=4a\left( y-\beta \right)$. We find the number of x intercepts and the value of the y intercept putting the values of $y=0$ and $y=0$ respectively. Also using the graph, we find the endpoints’ behaviour.

Complete step by step answer:
The given equation $y={{x}^{2}}-4$ is a parabolic curve. We equate it with the general equation of parabola ${{\left( x-\alpha \right)}^{2}}=4a\left( y-\beta \right)$.
For the general equation $\left( \alpha ,\beta \right)$ is the vertex. 4a is the length of the latus rectum.
Now we convert the given equation $y={{x}^{2}}-4$ according to the general equation to find the value of the vertex.
We get
$\begin{aligned} & y={{x}^{2}}-4 \\\ & \Rightarrow {{\left( x-0 \right)}^{2}}=\left( y+4 \right) \\\ \end{aligned}$
This gives the vertex as $\left( 0,-4 \right)$. The length of the latus rectum is $4a=1$.
We have to find the possible number of x intercepts and the value of the y intercept. The curve cuts the X and Y axis at certain points and those are the intercepts.
We first find the Y-axis intercepts. In that case for the Y-axis, we have to take the coordinate values of x as 0. Putting the value of $x=0$ in the equation $y={{x}^{2}}-4$, we get
$y={{0}^{2}}-4=-4$
The intercept is the point $\left( 0,-4 \right)$. The vertex is the intercept and it’s the only intercept on the Y-axis.
We first find the X-axis intercepts. In that case for X-axis, we have to take the coordinate values of y as 0. Putting the value of $y=0$ in the equation $y={{x}^{2}}-4$, we get
$\begin{aligned} & 0={{x}^{2}}-4 \\\ & \Rightarrow {{x}^{2}}=4 \\\ & \Rightarrow x=\pm 2 \\\ \end{aligned}$
The intercept points are $\left( \pm 2,0 \right)$. There are two intercepts on X-axis.

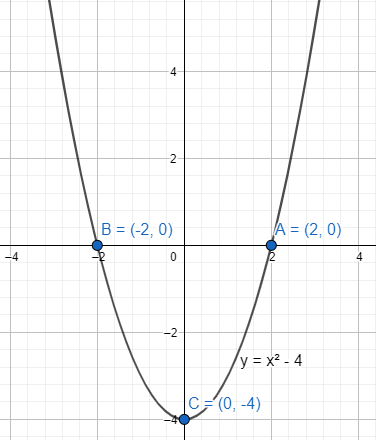
The end points of the curve are at infinity. As $x\to \pm \infty$ the value of $y\to \infty$. Y is a dependent function of x where $y={{x}^{2}}-4$. We put the values of x to find the endpoints' behaviour.

Note:
The minimum point of the function $y={{x}^{2}}-4$ is $y=-4$. The graph is bounded at that point. But on the other side the curve is open and not bounded. The general case of a parabolic curve is to be bounded at one side to mark the vertex.