Question

How do you find the end behavior of $y=-{{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}+6x+8$ ?

Answer 1

We need to find the end behavior of the polynomial $y=-{{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}+6x+8$ . We start to solve the problem by finding the limits at $-\infty$ and $+\infty$ for the given polynomial. Then, we evaluate and simplify the limits to get the required result.

Complete step by step solution:
We are given a polynomial and need to find the end behavior of it. We will be solving this question by finding out the value of the limit of the given polynomial at negative infinity and positive infinity.
The end behavior of a polynomial is the behavior of the polynomial or the function when it approaches negative infinity or positive infinity.
The degree of the polynomial is the highest of the degrees of all the individual terms in a polynomial. It is the highest power of the variable in the polynomial.
The coefficient in a polynomial is the numerical value multiplied to a variable.
For Example,
$\Rightarrow 6x$
Here,
6 is the coefficient
$x$ is the variable
The term with the highest degree in the polynomial is called the leading term of the polynomial.
The degree and the leading coefficient of the polynomial determine the end behavior of the function.
Evaluating the limit of the given polynomial at positive infinity, we get,
$\Rightarrow \displaystyle \lim_{x \to +\infty }\left( y \right)$
Substituting the value of y, we get,
$\Rightarrow \displaystyle \lim_{x \to +\infty }\left( -{{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}+6x+8 \right)$
From the above, we know that the leading coefficient will determine the end behavior of the whole function.
The leading term in the given polynomial is $-{{x}^{4}}$
Evaluating the limit for the leading term of the polynomial, we get,
$\Rightarrow \displaystyle \lim_{x \to +\infty }\left( -{{x}^{4}} \right)$
Substituting the value of limit in the above polynomial,
$\Rightarrow \displaystyle \lim_{x \to +\infty }\left( -{{x}^{4}} \right)=-\infty$
$\therefore \displaystyle \lim_{x \to +\infty }\left( -{{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}+6x+8 \right)=-\infty$
Evaluating the limit of the given polynomial at negative infinity, we get,
$\Rightarrow \displaystyle \lim_{x \to -\infty }\left( y \right)$
$\Rightarrow \displaystyle \lim_{x \to -\infty }\left( -{{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}+6x+8 \right)$
From the above, we know that the leading coefficient will determine the end behavior of the whole function.
The leading term in the given polynomial is $-{{x}^{4}}$
Evaluating the limit for the leading term of the polynomial, we get,
$\Rightarrow \displaystyle \lim_{x \to -\infty }\left( -{{x}^{4}} \right)$
Substituting the value of limit in the above polynomial,
$\Rightarrow \displaystyle \lim_{x \to -\infty }\left( -{{x}^{4}} \right)=-\infty$
$\therefore \displaystyle \lim_{x \to -\infty }\left( -{{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}+6x+8 \right)=-\infty$

Therefore, the value of the limit of the given polynomial at negative and positive infinity is negative infinity.

Note: The given question can be solved alternately by plotting the graph of the polynomial. The graph of the polynomial is given as follows,

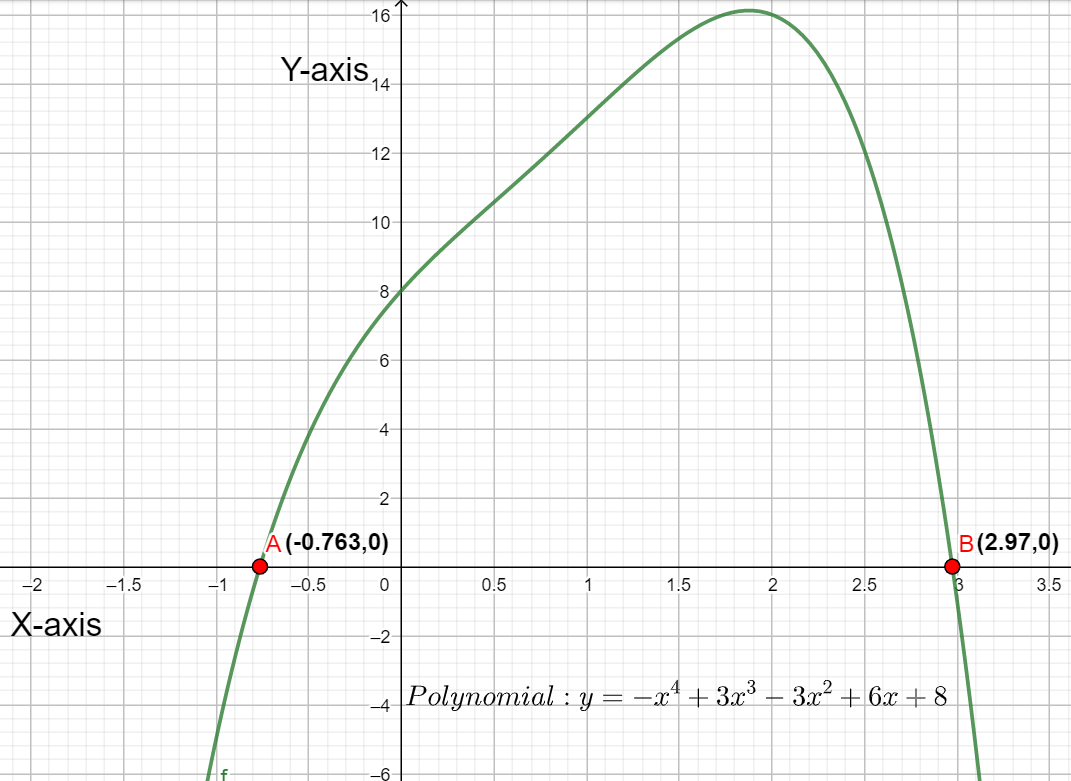
From the above graph,
We can say that the polynomial y approaches $-\infty$ when the value of $x$ approaches $-\infty$ or $+\infty$