Solveeit Logo
Login

Question

Question: How do you find the domain of \(f\left( x \right) = \dfrac{{4{x^2} - 9}}{{{x^2} + 5x + 6}}\)?...

How do you find the domain of f(x)=4x2−9x2+5x+6f\left( x \right) = \dfrac{{4{x^2} - 9}}{{{x^2} + 5x + 6}}?

Explanation

Solution

This is a simple question based on function and its domain set and codomain set. As we know that the domain of f(x)f\left( x \right) is the set of all those real numbers for which f(x)f\left( x \right) is meaningful. For this, determine the domain of the real function f(x)f\left( x \right) by finding all those real numbers for which the expression for f(x)f\left( x \right) or the formula for f(x)f\left( x \right) assumes real values only.

Complete step by step answer:
Given function: f(x)=4x2−9x2+5x+6f\left( x \right) = \dfrac{{4{x^2} - 9}}{{{x^2} + 5x + 6}}
We have to find the domain of a given function.
First understand the concept of domain, then determine the domain of given function.
Since we know that the domain of the real function f(x)f\left( x \right) is the set of all those real numbers for which the expression for f(x)f\left( x \right) or the formula for f(x)f\left( x \right) assumes real values only. In other words, the domain of f(x)f\left( x \right) is the set of all those real numbers for which f(x)f\left( x \right) is meaningful.
Here, f(x)=4x2−9x2+5x+6f\left( x \right) = \dfrac{{4{x^2} - 9}}{{{x^2} + 5x + 6}}
Clearly, f(x)f\left( x \right) is a rational function of xx as 4x2−9x2+5x+6\dfrac{{4{x^2} - 9}}{{{x^2} + 5x + 6}} is a rational expression in xx. We observe that f(x)f\left( x \right) assumes real values for all xx except for all those of xx for which x2+5x+6=0{x^2} + 5x + 6 = 0.
We are using the split middle term method.
x2+5x+6=0{x^2} + 5x + 6 = 0 writing the middle term in terms of 2x,3x2x,3x.
x2+2x+3x+6=0{x^2} + 2x + 3x + 6 = 0
Now, taking the common
x(x+2)+3(x+2)=0x\left( {x + 2} \right) + 3\left( {x + 2} \right) = 0
⇒(x+2)(x+3)=0\Rightarrow \left( {x + 2} \right)\left( {x + 3} \right) = 0
⇒x=−2,−3\Rightarrow x = - 2, - 3
Hence, Domain (ff) = \mathbb{R} - \left\\{ { - 2, - 3} \right\\}.

Therefore, the domain of given function is \mathbb{R} - \left\\{ { - 2, - 3} \right\\}.

Note: In above question, we can determine the domain of a given question by simply drawing the graph of the function.

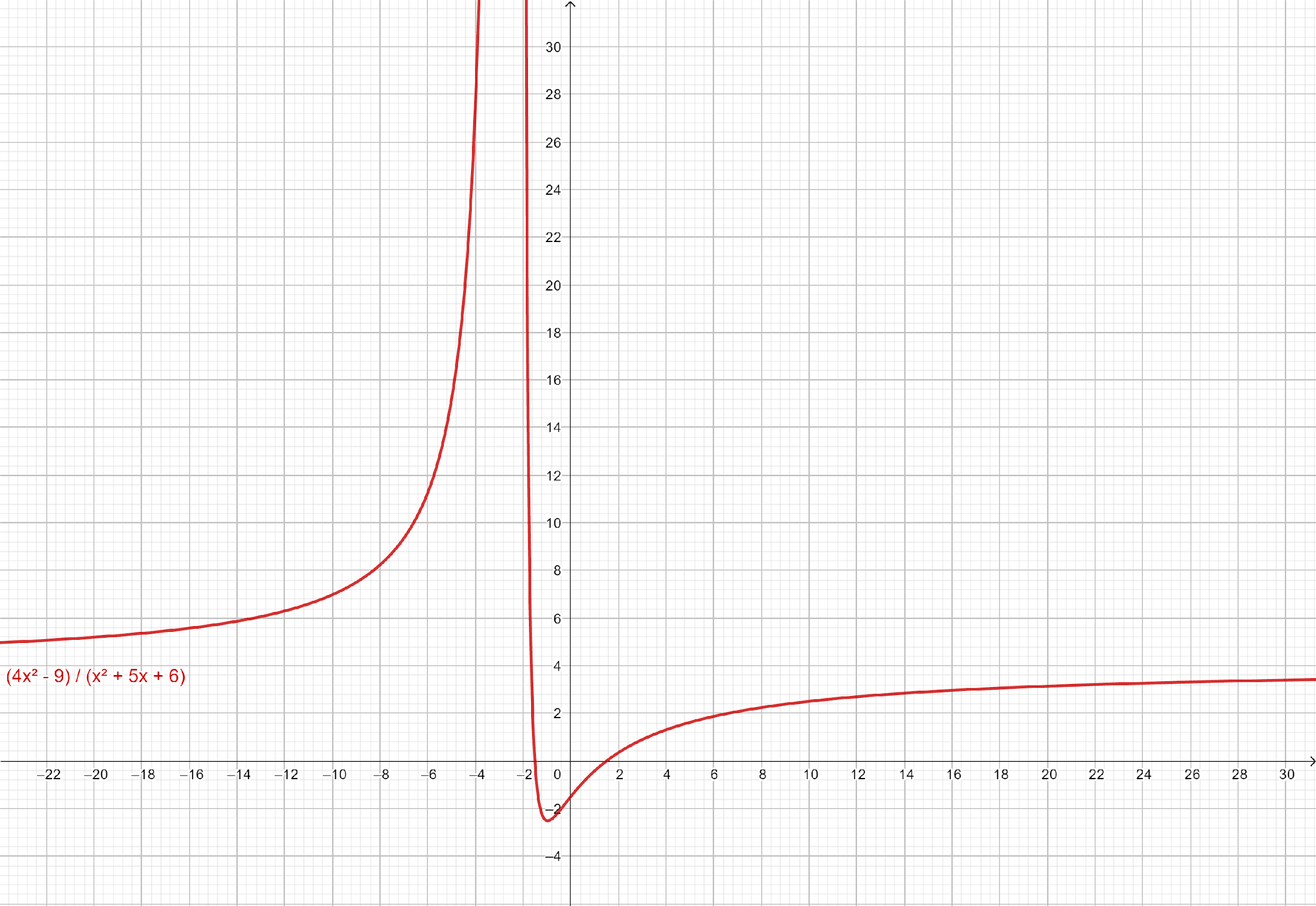
Therefore, the domain of a given function is \mathbb{R} - \left\\{ { - 2, - 3} \right\\}.