Question

How do you find the domain and range of $f\left( x \right) = \sqrt {x - 2}$?

Answer 1

First, determine the domain of the real function $f\left( x \right)$ by finding all those real numbers for which the expression for $f\left( x \right)$ or the formula for $f\left( x \right)$ assumes real values only. Next, determine the range of the given function. For this, put $y = f\left( x \right)$ and solve the equation $y = f\left( x \right)$ for $x$ in terms of $y$. Next, put $x = \phi \left( y \right)$ and find the values of $y$ for which the values of $x$, obtained from $x = \phi \left( y \right)$, are real and in the domain of $f$. Thus, the set of values of $y$ obtained is the range of $f$.

Formula used:
Domain of real functions:
The domain of the real function $f\left( x \right)$ is the set of all those real numbers for which the expression for $f\left( x \right)$ or the formula for $f\left( x \right)$ assumes real values only. In other words, the domain of $f\left( x \right)$ is the set of all those real numbers for which $f\left( x \right)$ is meaningful.
Range of real functions:
The range of a real function of a real variable is the set of all real values taken by $f\left( x \right)$ at points in its domain. In order to find the range of a real function $f\left( x \right)$, we may use the following algorithm.
Algorithm:
Step I Put $y = f\left( x \right)$.
Step II Solve the equation $y = f\left( x \right)$ for $x$ in terms of $y$. Let $x = \phi \left( y \right)$.
Step III Find the values of $y$ for which the values of $x$, obtained from $x = \phi \left( y \right)$, are real and in the domain of $f$.
Step IV The set of values of $y$ obtained in step III is the range of $f$.

Complete step by step solution:
Given function: $f\left( x \right) = \sqrt {x - 2}$
We have to find the domain and range of a given function.
First understand the concept of domain, then determine the domain of given function.
Since we know that the domain of the real function $f\left( x \right)$ is the set of all those real numbers for which the expression for $f\left( x \right)$ or the formula for $f\left( x \right)$ assumes real values only. In other words, the domain of $f\left( x \right)$ is the set of all those real numbers for which $f\left( x \right)$ is meaningful.
Here, $f\left( x \right) = \sqrt {x - 2}$
Clearly, $f\left( x \right)$ assumes real values, if
$x - 2 \geqslant 0$
$\Rightarrow x \geqslant 2$
$\Rightarrow x \in \left[ {2,\infty } \right)$
Hence, Domain ($f$) $= \left[ {2,\infty } \right)$.
Now, determine the range of the given function.
For this, put $y = f\left( x \right)$ and solve the equation $y = f\left( x \right)$ for $x$ in terms of $y$.
$\Rightarrow y = \sqrt {x - 2}$
Square both sides of the equation, we get
$\Rightarrow {y^2} = x - 2$
$\Rightarrow x = {y^2} + 2$
Now, put $x = \phi \left( y \right)$ and find the values of $y$ for which the values of $x$, obtained from $x = \phi \left( y \right)$, are real and in the domain of $f$.
Clearly, Range ($f$) $= \left[ {0,\infty } \right)$.

Therefore, the domain of given function is $\left[ {2,\infty } \right)$ and range is $\left[ {0,\infty } \right)$.

Note: In above question, we can determine the domain and range of a given question by simply drawing the graph of the function.

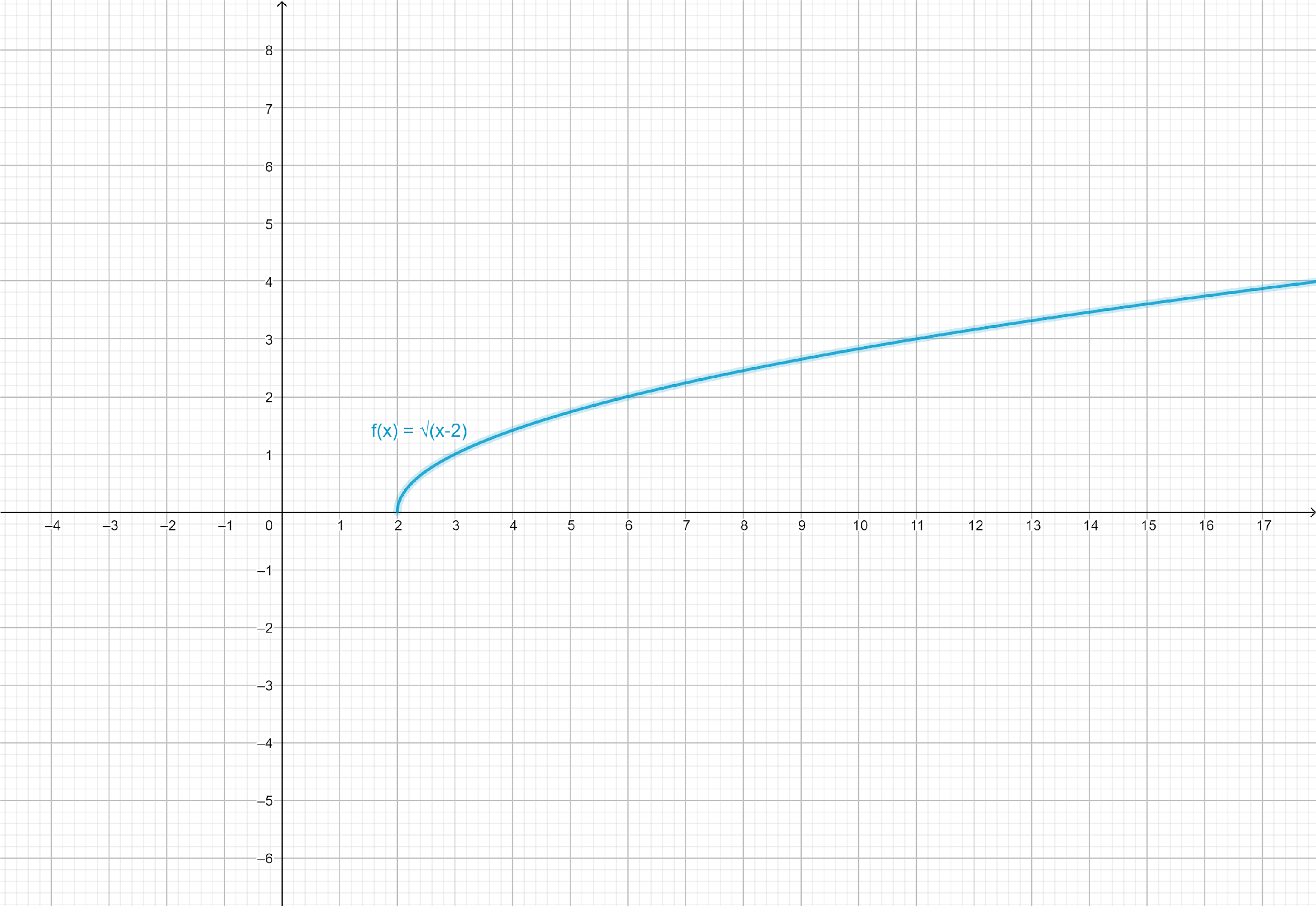
Final solution: Therefore, the domain of given function is $\left[ {2,\infty } \right)$ and range is $\left[ {0,\infty } \right)$.