Question

How do you find the domain and range for $y=4x+2$?

Answer 1

From the question given we have to find the domain and range or $y=4x+2$ . We know that the domain and range of the linear function are all real functions. Domain of the function means set off all the possible inputs to the function. Range of the function means the set of all the possible outputs to the function.

Complete step by step solution:
From the question given we have the function
$\Rightarrow y=4x+2$
First, we will find the domain of the function. We know that the domain of the function means set off all the possible inputs to the function.
Here in the above function the input values will be given to the x. We can give any value for the x in the above function so the domain of the function is all real numbers.
$\Rightarrow \left( -\infty ,\infty \right)$
So, the domain of the function $y=4x+2$ is all real numbers i.e., $\left( -\infty ,\infty \right)$.
Now, we have to find the range of the function. We know that range of the function means set off all the possible outputs for the given possible inputs to the function.
As, we know that the inputs i.e., domain of the function is all real numbers therefore the outputs will also be all real numbers.
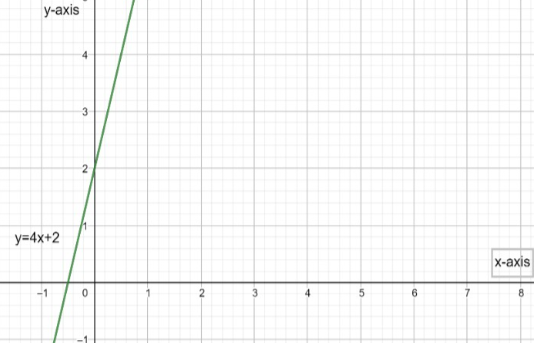
We can say it by also seeing the graph of the given function $y=4x+2$.
Therefore, by seeing the graph we can say that the domain and range of the function $y=4x+2$ is $\left( -\infty ,\infty \right)$i.e., all real numbers.

Note:
Students should know that in the general domain and range of a linear function, $y=mx+b$, are all real numbers. Any number x can be plugged in, and any output y can result, positive or negative. Students should also know about how to draw graphs for any given function.