Question

How do you find the domain and range for $\sec \theta$?

Answer 1

Domain and the range can be found by using graphs. We can find domain and range without using a graph also. In this method, we need to find the values of the given term. The given function might not be defined at some points hence we exclude those points. Similarly by checking the values of the function in the domain we will get the range of the function.

Complete step-by-step solution:
$\sec \theta$ is the given function. As mentioned in the question, we must find the domain and the range.
Let’s us consider the function$y=\sec \left( \theta \right)$
We all know that
$\sec \theta =\dfrac{1}{\cos \theta }$
Now we know that the denominator of any fraction cannot be zero. Hence let us check the values for which cos is 0. Now we know $\cos \theta =0$ only when $\theta$ has the values of $\dfrac{\pi }{2},\dfrac{3\pi }{2},\dfrac{5\pi }{2}$……
Here the general value of theta when
$\Rightarrow \cos \theta =0$ if $\theta =\left( k+\dfrac{1}{2} \right)\pi$ , for $k\in z$
Hence the domain of $\sec \theta$ is R-\left\\{ x ; x=\left( k+\dfrac{1}{2} \right)\pi ,k\in N \right\\}.
Now we know that $\cos \theta$ lies between -1 and 1.
$-1\le \cos \theta \le 1$
In graphical representation we get,

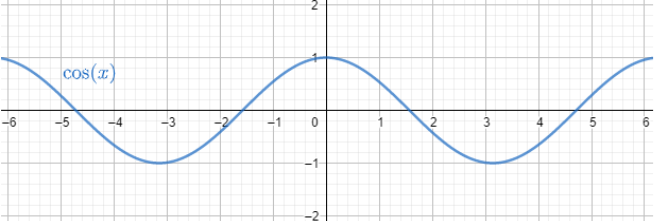
Now consider the function $y=\dfrac{1}{x}$ for $-1\le x\le 1$ we have $y\ge 1$ or $y\le -1$.
Hence if we have $y=\sec \left( \theta \right)$
$\sec \theta \ge 1$ Or$\sec \theta \le -1$.
Hence the range of $\sec \theta$ is $\left( -\infty ,1 \right]\cup \left[ 1,\infty \right)$
Now let us check the graph is the function $\sec \theta$

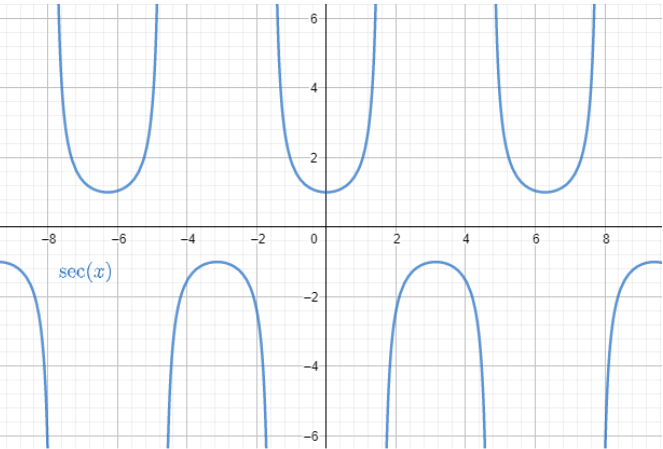
Hence the domain and range $\sec \theta$ are
Domain= R-\left\\{ x ; x=\left( k+\dfrac{1}{2} \right)\pi ,k\in N \right\\}
Range=$\left( -\infty ,1 \right]\bigcup \left[ 1,\infty \right)$

Note: The range and domain are noted in different brackets. The domain is represented in the curly bracket because the term inside the bracket is a formula. The range is represented with two types of brackets : square bracket and parenthesis bracket. The value which is written beside the square bracket is included as the endpoint whereas the value which is written beside the parenthesis bracket is not included as the endpoint.