Question

How do you find the dimensions of the rectangle with the largest area that can be inscribed in a semi – circle of radius r?

Answer 1

Draw a rough diagram of a semi – circle of radius ‘r’ and inscribe a rectangle in it such that one side of the rectangle lies on the diameter of the semi – circle and two vertices lie on its curved boundary. Join the centre of this semi – circle with the two vertices. Assume the length of the rectangle as ‘l’ while breadth as ‘b’. Now, use Pythagoras theorem given as: - ${{h}^{2}}={{b}^{2}}+{{p}^{2}}$, where h = hypotenuse, b = base and p = perpendicular, to find a relation between r, l and b. Use the formula: - Area = $l\times b$ to find the area of the rectangle. Now, substitute the value of l, in terms of r and b, in the area relation. Differentiate the area relation with respect to b and equate it equal to 0 and find the value of b in terms of r. Finally, substitute this value of b in Pythagoras relation to get the value of l in terms of r.

Complete step-by-step solution:
Here, we have been provided with a semi – circle of radius r and we have been asked to find the dimensions of the rectangle that will have maximum area when inscribed in this semi – circle.
Now, for the inscribed rectangle to have maximum area, its one side must lie on the diameter and the two vertices on the curved boundary of the semi – circle. So, let us draw a rough diagram of the given situation.

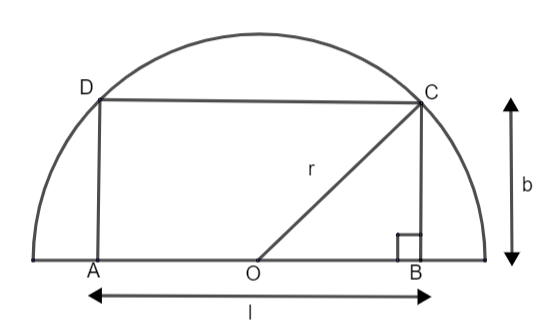
In the above figure, we have assumed l and b as the length and breadth of the rectangle respectively. Length l is divided into two equal parts at centre of the semi – circle. We have joined the centre (O) with vertex C.
Now, clearly we can see that OBC is a right angle triangle. So, applying the Pythagoras theorem given as: - ${{h}^{2}}={{b}^{2}}+{{p}^{2}}$, where h = hypotenuse, b = base and p = perpendicular, we get,

& \Rightarrow {{r}^{2}}={{b}^{2}}+{{\left( \dfrac{l}{2} \right)}^{2}} \\\ & \Rightarrow {{r}^{2}}={{b}^{2}}+\dfrac{{{l}^{2}}}{4} \\\ \end{aligned}$$ $$\Rightarrow 4\left( {{r}^{2}}-{{b}^{2}} \right)={{l}^{2}}$$ - (1) We know that area of a rectangle is the product of its length and breadth, let us denoted the area with A, so we have, $$\Rightarrow A=l\times b$$ Substituting the value of l from equation (1), we get, $$\Rightarrow A=\sqrt{4\left( {{r}^{2}}-{{b}^{2}} \right)}\times b$$ On squaring both the sides, we get, $$\begin{aligned} & \Rightarrow {{A}^{2}}=4\left( {{r}^{2}}-{{b}^{2}} \right)\times {{b}^{2}} \\\ & \Rightarrow {{A}^{2}}=4\left( {{r}^{2}}{{b}^{2}}-{{b}^{4}} \right) \\\ \end{aligned}$$ Now, for the area to be maximum, its derivative must be 0. Here, in the above relation we have area as a function of b and r is a constant, so differentiating both the sides with respect to the variable b, we get, $$\begin{aligned} & \Rightarrow \dfrac{d\left[ {{A}^{2}} \right]}{db}=\dfrac{d\left[ 4\left( {{r}^{2}}{{b}^{2}}-{{b}^{4}} \right) \right]}{db} \\\ & \Rightarrow 2A\dfrac{dA}{db}=4\left[ {{r}^{2}}\times 2b-4{{b}^{3}} \right] \\\ & \Rightarrow \dfrac{dA}{db}=\dfrac{2}{A}\left[ 2b{{r}^{2}}-4{{b}^{3}} \right] \\\ \end{aligned}$$ Substituting $$\dfrac{dA}{db}=0$$, we get, $$\begin{aligned} & \Rightarrow \dfrac{2}{A}\left[ 2b{{r}^{2}}-4{{b}^{3}} \right]=0 \\\ & \Rightarrow 2b{{r}^{2}}-4{{b}^{3}}=0 \\\ & \Rightarrow 2{{r}^{2}}-4{{b}^{2}}=0 \\\ & \Rightarrow {{r}^{2}}=2{{b}^{2}} \\\ & \Rightarrow {{b}^{2}}=\dfrac{{{r}^{2}}}{2} \\\ \end{aligned}$$ Taking square root both the sides, we get, $$\Rightarrow b=\dfrac{r}{\sqrt{2}}$$ Now, substituting the value of b in equation (1), we get, $$\Rightarrow {{l}^{2}}=4\left( {{r}^{2}}-\dfrac{{{r}^{2}}}{2} \right)$$ $$\begin{aligned} & \Rightarrow {{l}^{2}}=\dfrac{4{{r}^{2}}}{2} \\\ & \Rightarrow {{l}^{2}}=2{{r}^{2}} \\\ \end{aligned}$$ Taking square root both the sides, we get, $$\Rightarrow l=\sqrt{2}r$$ **Hence, the dimensions of the rectangle with largest area that can be inscribed in a semi – circle of radius r are $$\sqrt{2}r\times \dfrac{r}{\sqrt{2}}$$.** **Note:** One may note that while differentiating the area relation we have considered radius ‘r’ as a constant because it is already given to us that the semi – circle has radius r and since we are not changing the semi – circle, the value of r will remain the same. Note that we have considered length l on the diameter of the circle, you can also consider base b on the diameter. This will not alter the dimensions.