Question

How do you find the derivative of ${(\tan x)^{ - 1}}?$

Answer 1

First look at the function they have given which is ${(\tan x)^{ - 1}}$, now we need to rewrite the function in order to find the derivative of the function. So ${(\tan x)^{ - 1}}$ can be written as $\dfrac{1}{{\tan x}}$ , now by using trigonometric ratios try to find what is $\dfrac{1}{{\tan x}}$ and find the derivative of that function.

Complete step by step solution:
First look at the function they have given which is ${(\tan x)^{ - 1}}$ , now we need to rewrite the function in order to find the derivative of the function. So ${(\tan x)^{ - 1}}$ can be written as $\dfrac{1}{{\tan x}}$.
Now by using trigonometric ratios try to find what is $\dfrac{1}{{\tan x}}$ to find the derivative of the function.
So consider the below triangle $ABC$ as shown,

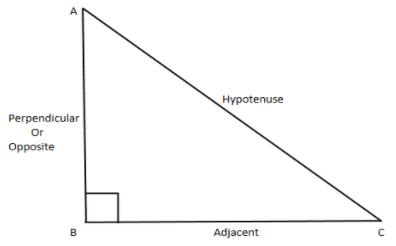
From the above diagram we have $AC = hypotenuse$ , $BC = Adjacent$ and $AB = Opposite$
So, now we can write the trigonometric ratios of functions as follows:
1: Sine function is given by: $\dfrac{{opposite}}{{hypotenuse}}$ .
2: Cosine function is given by: $\dfrac{{adjacent}}{{hypotenuse}}$.
3: Tangent function is given by: $\dfrac{{opposite}}{{adjacent}}$ .
4: Cosecant function is given by: $\dfrac{{hypotenuse}}{{opposite}}$ which is the inverse of sine function, so we can write it in terms of sine function as $\dfrac{1}{{\sin x}}$ .
5: Secant function is given by: $\dfrac{{hypotenuse}}{{adjacent}}$ which is the inverse of cosine function, so we can write it in terms of cosine function as $\dfrac{1}{{\cos x}}$ .
6: Cotangent function is given by: $\dfrac{{adjacent}}{{opposite}}$ which is the inverse of tangent function, so we can write it in terms of tangent function as $\dfrac{1}{{\tan x}}$.
By the above discussion of trigonometric ratios $\dfrac{1}{{\tan x}} = \cot x$
Now differentiate the function $\cot x$ ,
That is $\dfrac{d}{{dx}}\cot x$
We know that the derivative of $\cot x$ is $- {\csc ^2}x$.

Therefore the answer for the given question is $- {\csc ^2}x$

Note:
When finding the derivative of $\cot x$ , if you don’t know the derivative of that then try to rewrite the function as $\cot x = \dfrac{{\cos x}}{{\sin x}}$ and now apply quotient rule to simplify and find the derivative of the same function, you will get the same as above.