Question

How do you find the critical points to graph $y=\sin \left( \dfrac{x}{2} \right)$?

Answer 1

In this problem we need to calculate the critical point on the given curve. We know that the critical points are the points on the curve at which the curve has maximum, minimum and zero values. So, we will assume the range of variable $x$ based on the given function and calculate all the known values in the given interval. Now we will plot the graph of the given equation and observe the critical points.

Complete step by step solution:
Given that, $y=\sin \left( \dfrac{x}{2} \right)$.
In the given equation we can observe the trigonometric function $\sin$. We know that the function $\sin x$ shows unique value in the range of $\left[ 0,2\pi \right]$. But in the above equation we have $\sin \left( \dfrac{x}{2} \right)$ i.e., it shows the unique ranges in $\left[ 0\times 2,2\pi \times 2 \right]=\left[ 0,4\pi \right]$. So, considering the range of variables $x$ as $\left[ 0,4\pi \right]$. Now the value of $y$ for different values of $x$ will be
If $x=0\Rightarrow \sin \left( \dfrac{x}{2} \right)=\sin 0=0$
If $x=\dfrac{\pi }{2}\Rightarrow \sin \left( \dfrac{\dfrac{\pi }{2}}{2} \right)=\sin \left( \dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}$
If $x=\pi \Rightarrow \sin \left( \dfrac{\pi }{2} \right)=1$
If $x=\dfrac{3\pi }{2}\Rightarrow \sin \left( \dfrac{\dfrac{3\pi }{2}}{2} \right)=\sin \left( \dfrac{3\pi }{4} \right)=\dfrac{1}{\sqrt{2}}$
If $x=2\pi \Rightarrow \sin \left( \dfrac{2\pi }{2} \right)=\sin \pi =0$
If $x=\dfrac{5\pi }{2}\Rightarrow \sin \left( \dfrac{\dfrac{5\pi }{2}}{2} \right)=\sin \left( \dfrac{5\pi }{4} \right)=\dfrac{1}{\sqrt{2}}$
If $x=3\pi \Rightarrow \sin \left( \dfrac{3\pi }{2} \right)=-1$
If $x=\dfrac{7\pi }{2}\Rightarrow \sin \left( \dfrac{\dfrac{7\pi }{2}}{2} \right)=\sin \left( \dfrac{7\pi }{4} \right)=-\dfrac{1}{\sqrt{2}}$
If $x=4\pi \Rightarrow \sin \left( \dfrac{4\pi }{2} \right)=\sin 2\pi =0$
Plotting the graph of the function $y=\sin \left( \dfrac{x}{2} \right)$ from the above points, then we will get

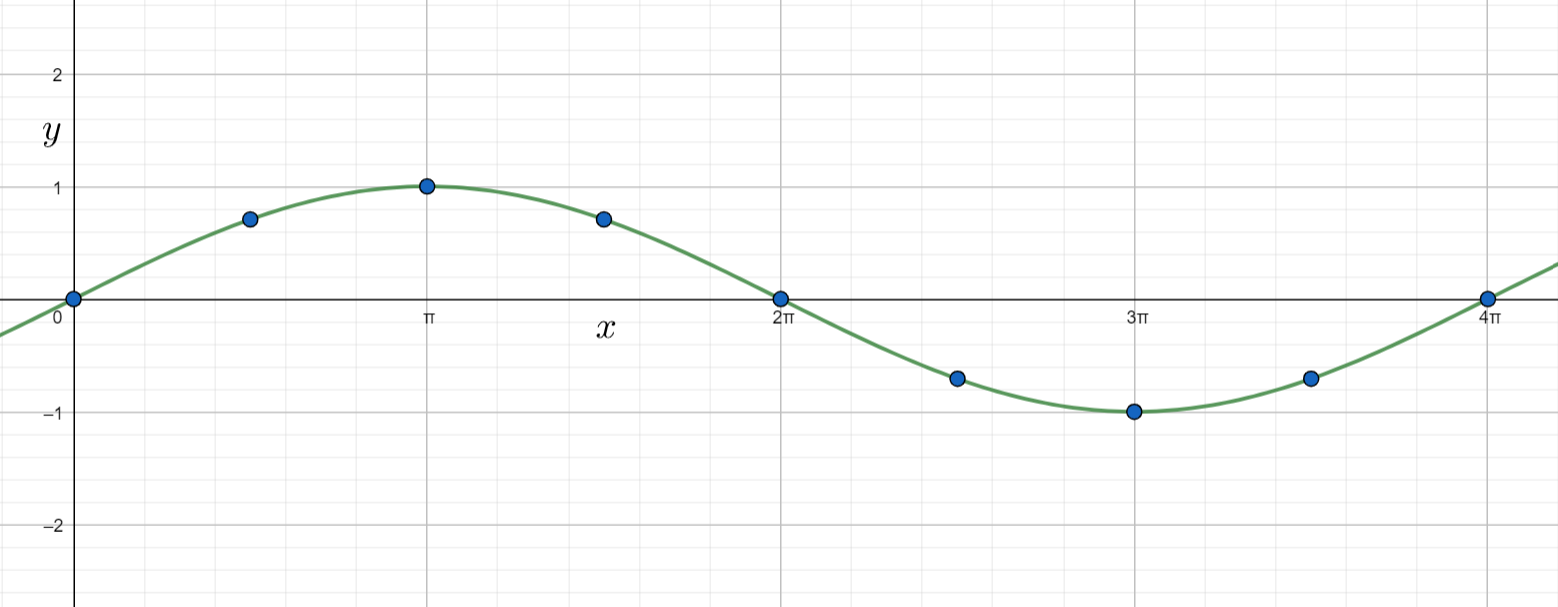
From the above graph we can say that the critical points are $0$, $\pi$, $2\pi$, $3\pi$, $4\pi$.
The zeros of the graph at $0$, $2\pi$, $4\pi$.
The maximum of the graph at $\pi$.
The minimum of the graph at $3\pi$.

Note: We can also calculate the critical point of the function $y=\sin \left( \dfrac{x}{2} \right)$ from the critical points of $y=\sin x$. The graph of the function $y=\sin x$ will be

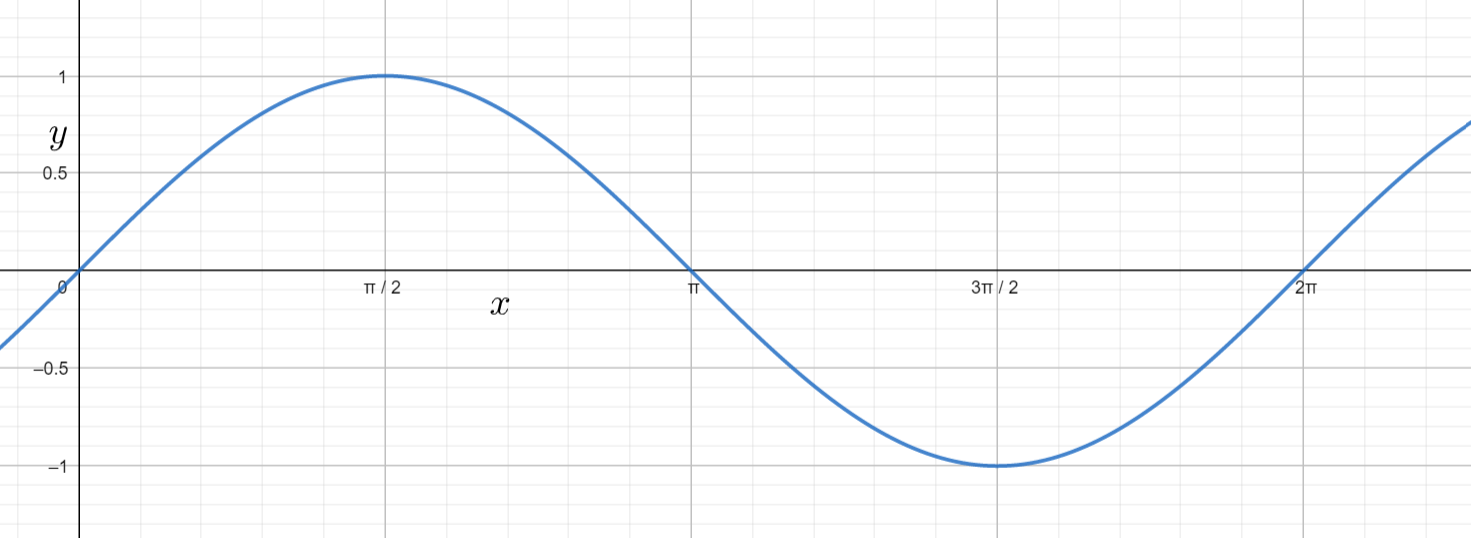
From the above graph the critical point of $y=\sin x$ are $0$, $\dfrac{\pi }{2}$, $\pi$, $\dfrac{3\pi }{2}$, $2\pi$. If we multiply the above values with two then we will get the critical point of $y=\sin \left( \dfrac{x}{2} \right)$.