Question

How do you find the critical points of $y=x-2\sin x$ on the interval $\left[ 0,\dfrac{\pi }{2} \right]$?

Answer 1

For this problem we need to calculate the critical point of the given function. We know that the critical points are the points which show either maximum, minimum or zero values for the given interval. So, we need to find the values of $x$ where the given function has maximum, minimum and zero values. For calculating the value of $x$ where the given function is zero, we will simply equate the given function to zero and simplify the equation to the one critical point. Now we will differentiate the given equation to find the remaining critical points.

Complete step by step solution:
Given that, $y=x-2\sin x$
Given interval $\left[ 0,\dfrac{\pi }{2} \right]$.
To find the value of $x$ where the given function is zero, equating the given function to zero, then we will get
$\begin{aligned} & \Rightarrow x-2\sin x=0 \\\ & \Rightarrow x=2\sin x \\\ & \Rightarrow \dfrac{x}{2}=\sin x \\\ \end{aligned}$
In the given interval $\left[ 0,\dfrac{\pi }{2} \right]$, we have only one value which satisfies the above equation is $x=0$. So $x=0$ is one critical point.
To check the maximum and minimum value of the given equation, we are going to differentiate the given equation with respect to $x$, then we will get
$\begin{aligned} & \Rightarrow \dfrac{dy}{dx}=\dfrac{d}{dx}\left( x-2\sin x \right) \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{d}{dx}\left( x \right)-2\dfrac{d}{dx}\left( \sin x \right) \\\ \end{aligned}$
Applying the known differentiation formulas, then we will have
$\Rightarrow \dfrac{dy}{dx}=1-2\cos x$
We can observe that we always get a negative differentiation value for all $x\in \left[ 0,\dfrac{\pi }{2} \right]$. So, the given function has a minimum value in the range of $x\in \left[ 0,\dfrac{\pi }{2} \right]$ and the value of $x$ at which the given function has minimum value is given by equating the differentiation value to zero, then we will have
$\begin{aligned} & \Rightarrow 1-2\cos x=0 \\\ & \Rightarrow 2\cos x=1 \\\ & \Rightarrow \cos x=\dfrac{1}{2} \\\ \end{aligned}$
In the range of $x\in \left[ 0,\dfrac{\pi }{2} \right]$ we have $\cos \dfrac{\pi }{3}=\dfrac{1}{2}$. Hence the function has minimum value at $x=\dfrac{\pi }{3}$.
Finally, the critical points on the given equation $y=x-2\sin x$ in the interval $x\in \left[ 0,\dfrac{\pi }{2} \right]$ are $0$, $\dfrac{\pi }{3}$.

Note: We can also check the graph of the given equation in the given interval to know the critical points. We can have the graph of the given equation as

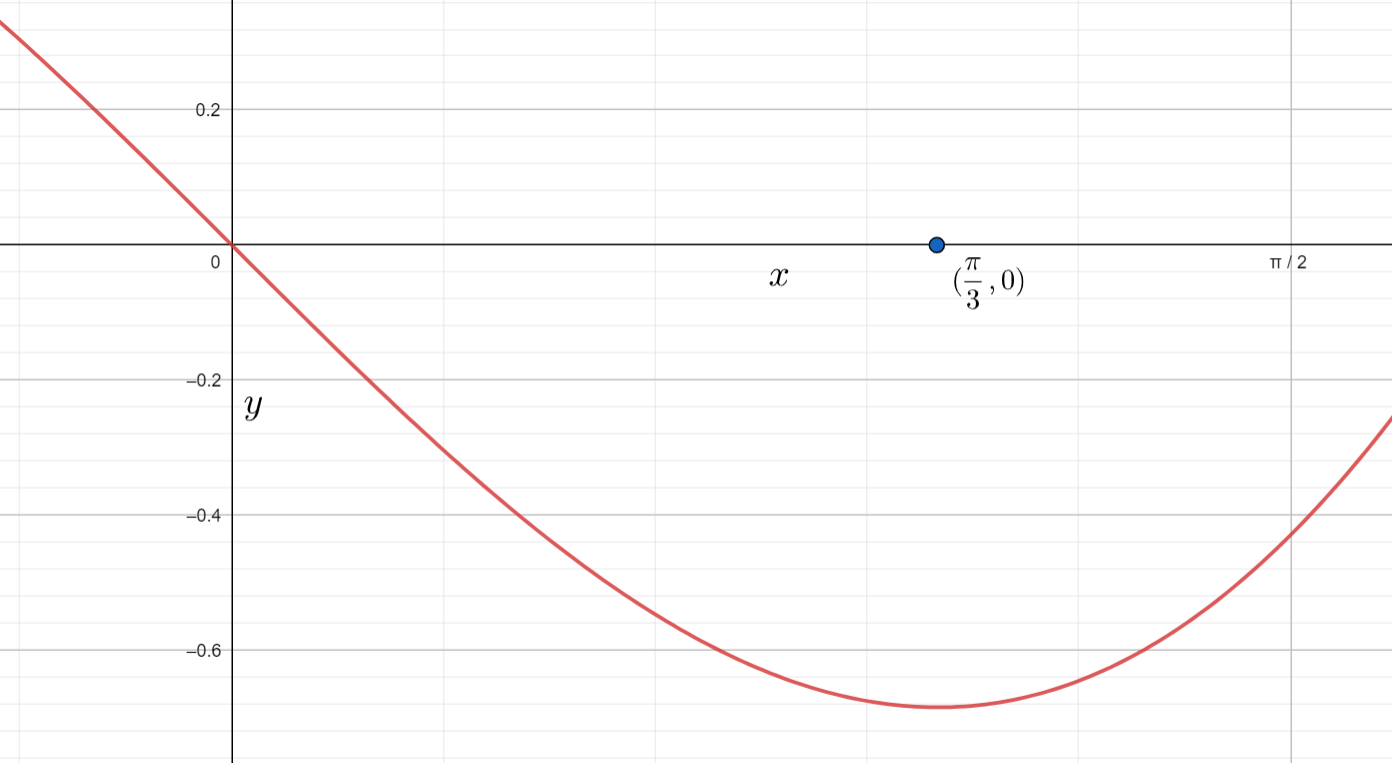
From the above graph also, we have the critical points at $0$, $\dfrac{\pi }{3}$.