Question

How do you find the critical points for $f\left( x \right)=3{{\sin }^{2}}x$ and the local max and min?

Answer 1

To find the critical points for $f\left( x \right)=3{{\sin }^{2}}x$ , we have to differentiate the function and equate it to 0. Then, we have to find the values of x. These are critical points. We will then substitute each values of x in the given function. If the function at the critical points are positive, and if the value of the function at the critical point is greater than zero, then that point will be the local maximum. If the value of the function at a critical point is less than or equal to 0, that point will be the local maximum.

Complete step-by-step answer:
We have to find the critical points for $f\left( x \right)=3{{\sin }^{2}}x$ and the local max and min. Let us first find the critical points. For this, we have to differentiate the given function with respect to x. We will have to apply chain rule to differentiate the given function.
$\begin{aligned} & f\left( x \right)=3{{\sin }^{2}}x \\\ & \Rightarrow f'\left( x \right)=3\times 2\sin x\cos x \\\ \end{aligned}$
We know that $\sin 2x=2\sin x\cos x$ . Hence, the above equation becomes $\Rightarrow f'\left( x \right)=3\sin 2x$
Now, to find the critical points, we will equate $f'\left( x \right)$ to 0.
$\begin{aligned} & \Rightarrow f'\left( x \right)=0 \\\ & \Rightarrow 3\sin 2x=0 \\\ \end{aligned}$
Let us take 3 from LHS to RHS.
$\Rightarrow \sin 2x=0$
We know that when $\sin x=0$ , $x=n\pi$ , where $n=0,1,2,...\text{ and }n\in Z$ . Hence, the above equation becomes
$\begin{aligned} & \Rightarrow 2x=n\pi \\\ & \Rightarrow 2x=0,\pi ,2\pi ,3\pi ,... \\\ \end{aligned}$
Now, let us take 2 from LHS to RHS.
$\Rightarrow x=\dfrac{\pi }{2},\pi ,\dfrac{3\pi }{2},2\pi ,..$
We can also denote x for negative values.
$\Rightarrow x=-\dfrac{\pi }{2},-\pi ,-\dfrac{3\pi }{2},-2\pi ,...$
In general, we can say that $x=\dfrac{n\pi }{2},n\in Z$ .
We have to consider the different values of x and substitute these in the given function.
Let us consider $x=0$ .
$\Rightarrow f\left( 0 \right)=3{{\sin }^{2}}0=0$
Let us now consider $x=\dfrac{\pi }{2}$ .
$\Rightarrow f\left( \dfrac{\pi }{2} \right)=3{{\sin }^{2}}\left( \dfrac{\pi }{2} \right)=3\times 1=3>0$
Now, we have to consider $x=\pi$ .
$\Rightarrow f\left( \pi \right)=3{{\sin }^{2}}\left( \pi \right)=0$
Let us consider $x=\dfrac{3\pi }{2}$ .
$\Rightarrow f\left( \dfrac{3\pi }{2} \right)=3{{\sin }^{2}}\left( \dfrac{3\pi }{2} \right)=3\times {{\left( -1 \right)}^{2}}=3>0$
We have to consider $x=2\pi$ .
$\Rightarrow f\left( 2\pi \right)=3{{\sin }^{2}}\left( 2\pi \right)=0$
Let us summarize this. We can see that the function is always positive. We can see that for $x=\dfrac{\left( 2n-1 \right)\pi }{2}$ , the value of the function is 3 which is greater than 0. Hence, local maximum is at 3 . AT $x=n\pi$ , the local minimum occurs. The local minimum point is 0. The graph is shown below.

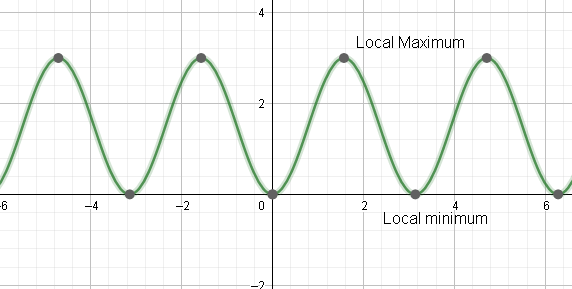
Hence, the critical points are $x=\dfrac{n\pi }{2},n\in Z$ ,local maximum is at $x=\dfrac{\left( 2n-1 \right)\pi }{2},n\in Z$ and the local maximum point is 3, and local minimum is at $x=n\pi ,n\in Z$ and the local minimum point is at 0.

Note: Students must know the first and second derivative tests to find the local maxima and local minima. The first derivative test includes a function f and $f\left( c \right)=0$ , then we can say that if f’(x) changes sign from positive to negative as x increases through point c, then c is the point of local maxima. And the f(c) is the maximum value. If f’(x) changes sign from negative to positive as x increases through point c, then c is the point of local minima. And the f(c) is the minimum value. If f’(x) doesn’t change sign as x increases through c, then c is neither a point of local nor a point of local maxima. It will be called the point of inflection.