Question

How do you find the critical numbers for $f\left( x \right)={{x}^{3}}+{{x}^{2}}+x$ to determine the maximum and the minimum?

Answer 1

We find the slope of the given function $f\left( x \right)={{x}^{3}}+{{x}^{2}}+x$. We equate it with 0. Extremum points in a curve have slope value 0. We solve the quadratic solution to find the coordinates and the points.

Complete step by step answer:
We need to find the relative extrema of the function $f\left( x \right)={{x}^{3}}+{{x}^{2}}+x$.
To find the extremum points we need to find the slope of the function and also the value of the point where the slope will be 0.
Extremum points in a curve have slope value 0.
The slope of the function $f\left( x \right)={{x}^{3}}+{{x}^{2}}+x$ can be found from the derivative of the function ${{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left[ f\left( x \right) \right]$.
We differentiate both sides of the function $f\left( x \right)={{x}^{3}}+{{x}^{2}}+x$ with respect to $x$.
$\begin{aligned} & f\left( x \right)={{x}^{3}}+{{x}^{2}}+x \\\ & \Rightarrow {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left[ f\left( x \right) \right]=\dfrac{d}{dx}\left[ {{x}^{3}}+{{x}^{2}}+x \right] \\\ \end{aligned}$.
We know that the differentiation form for ${{n}^{th}}$ power of $x$ is $\dfrac{d}{dx}\left[ {{x}^{n}} \right]=n{{x}^{n-1}}$.
Therefore, ${{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( {{x}^{3}} \right)+\dfrac{d}{dx}\left( {{x}^{2}} \right)+\dfrac{d}{dx}\left( x \right)=3{{x}^{2}}+2x+1$.
To find the $x$ coordinates of the extremum points we take $3{{x}^{2}}+2x+1=0$.
We know for a general equation of quadratic $a{{x}^{2}}+bx+c=0$, the value of the roots of x will be $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$.
In the given equation we have $3{{x}^{2}}+2x+1=0$. The values of $a,b,c$ is $3,2,1$ respectively.
We put the values and get $x$ as $x=\dfrac{-2\pm \sqrt{{{2}^{2}}-4\times 1\times 3}}{2\times 3}=\dfrac{-2\pm \sqrt{-8}}{6}=\dfrac{-1\pm i\sqrt{2}}{3}$.
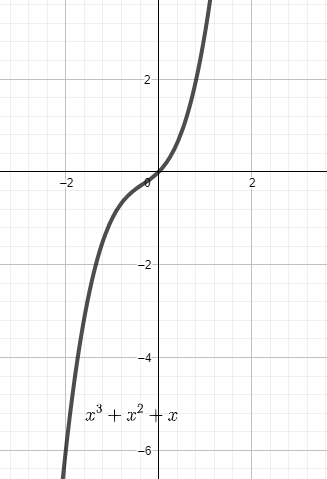
The roots of the slope are imaginary which means the curve $f\left( x \right)={{x}^{3}}+{{x}^{2}}+x$ has no extremum values.
${{f}^{'}}\left( x \right)=3{{x}^{2}}+2x+1$ is equation with value being greater than 0 as $3{{x}^{2}}+2x+1=2{{x}^{2}}+{{\left( x+1 \right)}^{2}}$ is sum of squares. So, ${{f}^{'}}\left( x \right)=3{{x}^{2}}+2x+1>0$.
In no points of the curve $f\left( x \right)={{x}^{3}}+{{x}^{2}}+x$ has slope value 0.

Note: We can also prove it from the graph of the curve $f\left( x \right)={{x}^{3}}+{{x}^{2}}+x$. This is an increasing function. There is no sharp curve in the graph to have slope 0.