Question

How do you find the coordinates of the centre, foci, the length of the major and minor axis given $16{{x}^{2}}+9{{y}^{2}}=144$ ?

Answer 1

We are given equation as $16{{x}^{2}}+9{{y}^{2}}=144$, we are asked to find centre, foci, length of major and minor axis, to find all this we will learn what type of equation in this, then we reduce it to standard form, we will reduce it to $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ then we will compare our equation with $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$ to find the value of $\left( h,k \right)$ centre also we find value of ‘a’ and ‘b’, using ‘a’ and ‘b’ we find length of major and minor axis, and we use $c=\pm \sqrt{{{b}^{2}}-{{a}^{2}}}$ , to find foci.

Complete step-by-step answer:
We are given a equation as $16{{x}^{2}}+9{{y}^{2}}=144$ , we are asked to find various things, to do so we will work on given equation, we have $16{{x}^{2}}+9{{y}^{2}}=144$ , here we can see that ${{x}^{2}}$ and ${{y}^{2}}$ are both being added and their coefficient are not same. So it is not a circle also coefficient of both are positive so it is not hyperbola.
So, we get our equation is ellipse.
Now we know that equation of ellipse is given as $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$ .
Where $\left( h,k \right)$ denote the centre of the ellipse, and ‘a’, ‘b’ represent half of the major/minor axis as in our problem, we have $16{{x}^{2}}+9{{y}^{2}}=144$.
We divide both sides by 144, to reduce it to standard form.
$\dfrac{16{{x}^{2}}}{144}+\dfrac{9{{y}^{2}}}{144}=\dfrac{144}{144}$ .
By simplifying, we get –
$\dfrac{{{x}^{2}}}{9}+\dfrac{{{y}^{2}}}{16}=1$ .
Now as $9={{3}^{2}}$ and $16={{4}^{2}}$ .
So, we can also re write it as –
$\dfrac{{{x}^{2}}}{{{3}^{2}}}+\dfrac{{{y}^{2}}}{{{4}^{2}}}=1$ .
As our standard form is $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$ , so we can also write it as $\dfrac{{{\left( x-0 \right)}^{2}}}{{{3}^{2}}}+\dfrac{{{\left( y-0 \right)}^{2}}}{{{4}^{2}}}=1$ .
So, comparing this with our standard equation, we get –
$h=0,k=0$
And value of $a=3,b=4$ .
As $h=0,k=0$ so coordinate of centre is $\left( h,k \right)=\left( 0,0 \right)$ .
So, coordinate of centre $=\left( 0,0 \right)$ .
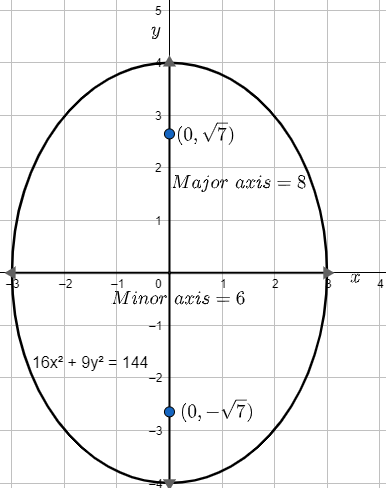
Now, here $aAs ‘a’ is having length of minor axis so length of minor axis$=2a$As$a=3$so, length of minor axis$=2\times 3=6$. Similarly, b-denotes giving the length of major axis So, length of major axis$=2b$$\begin{aligned}
& =2\times 4 \\
& =8 \\
\end{aligned}$(as$b=4$) Now foci of the ellipse is given as$c=\pm \sqrt{{{b}^{2}}-{{a}^{2}}}$(major – minor). As$b=4$and$a=3$so, Using these we get –$\begin{aligned}
& c=\pm \sqrt{{{4}^{2}}-{{3}^{2}}} \\
& =\pm \sqrt{16-9} \\
& c=\pm \sqrt{7} \\
\end{aligned}$. So, foci is$\pm \sqrt{7}$. As major axis is ‘y’. So, coordinate of foci is$\left( 0,+\sqrt{7} \right)$and$\left( 0,-\sqrt{7} \right)$ .

Note: Remember that here for foci, we subtract the square of major axis from square of minor axis so if ‘x’ is major and ‘y’ is minor then we get foci $=\pm \sqrt{{{a}^{2}}-{{b}^{2}}}$ , also we always careful that we consider both options ‘+’ and ‘-‘ for foci as in ellipse we have two focus.