Question

How do you find the coordinates of the center of a circle whose equation is ${{(x+11)}^{2}}+{{(y-13)}^{2}}=4$ ?

Answer 1

In this question we will convert the expression into the general form of the equation of a circle which is denoted as ${{(x-a)}^{2}}+{{(y-a)}^{2}}={{r}^{2}}$, where $(a,b)$ is the center of the circle and $r$ is the radius of the circle. In this question we will deduce the points $a$ and $b$ from the given equation.

Complete step by step answer:
We have the equation of the circle as ${{(x+11)}^{2}}+{{(y-13)}^{2}}=4$.
We can write the left-hand side of the expression as:
${{(x-(11))}^{2}}+{{(y-13)}^{2}}=4$
Now we know that ${{2}^{2}}=4$ therefore, on substituting it in the right-hand side of the expression, we get:
${{(x-(11))}^{2}}+{{(y-13)}^{2}}={{2}^{2}}$
Now the above is in the form of the general equation of the circle which is ${{(x-a)}^{2}}+{{(y-a)}^{2}}={{r}^{2}}$, where $(a,b)$ is the center of the circle and $r$ is the radius of the circle.
From the equation of the circle, we can deduce that the value of $a=-11$, $b=13$ and the radius of the circle is $2$.
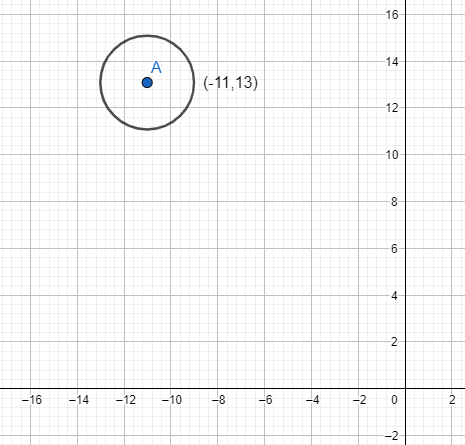
Therefore, the center of the circle is $(-11,13)$, which is the required solution.
The circle be plotted on the graph as:

Note: The equation of a circle should be remembered while doing these types of questions
it is to be remembered that adding and subtracting values on both sides of the $=$ sign, the value of the equation does not change.
The equation of a circle with its center at the origin is generally used. Since the origin is $0$, the equation is ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ where $r$ is radius of the circle.
It is to be remembered that the diameter of the circle is two times the radius of the circle. It can be written as $2r=d$.