Question

How do you find the continuity of a function on a closed interval?

Answer 1

Continuity of function in a closed interval $\left[ {a,b} \right]$: A function $f$ is said to be continuous on a closed interval $\left[ {a,b} \right]$ if
$f$ is continuous on $\left( {a,b} \right)$.
$f$ is continuous from the right at $a$, i.e., $\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right)$, and
$f$ is continuous from the left at $b$, i.e., $\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)$.

Complete step by step solution:
First, we will discuss the continuity on a closed interval.
Continuity on a closed interval: A function $f\left( x \right)$ is said to be continuous on a closed interval $\left[ {a,b} \right]$ if and only if
$f$ is continuous on the open interval $\left( {a,b} \right)$
$\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right)$, and
$\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)$
In other words, $f\left( x \right)$ is continuous on $\left[ {a,b} \right]$ if and only if it is continuous on $\left( {a,b} \right)$ and it continuous at $a$ from the right and at $b$ from the left.
Final solution: Hence, to determine if a function is continuous or not on a closed interval we check if the function is continuous or not in a closed interval, and it is continuous at endpoints from the right and left.

Note: Consider the function
$f\left( x \right) = 1$ if $x \leqslant 0$ and $f\left( x \right) = 0$ if $x > 0$
This function is of course defined at every point of the real line. Graph of this function is

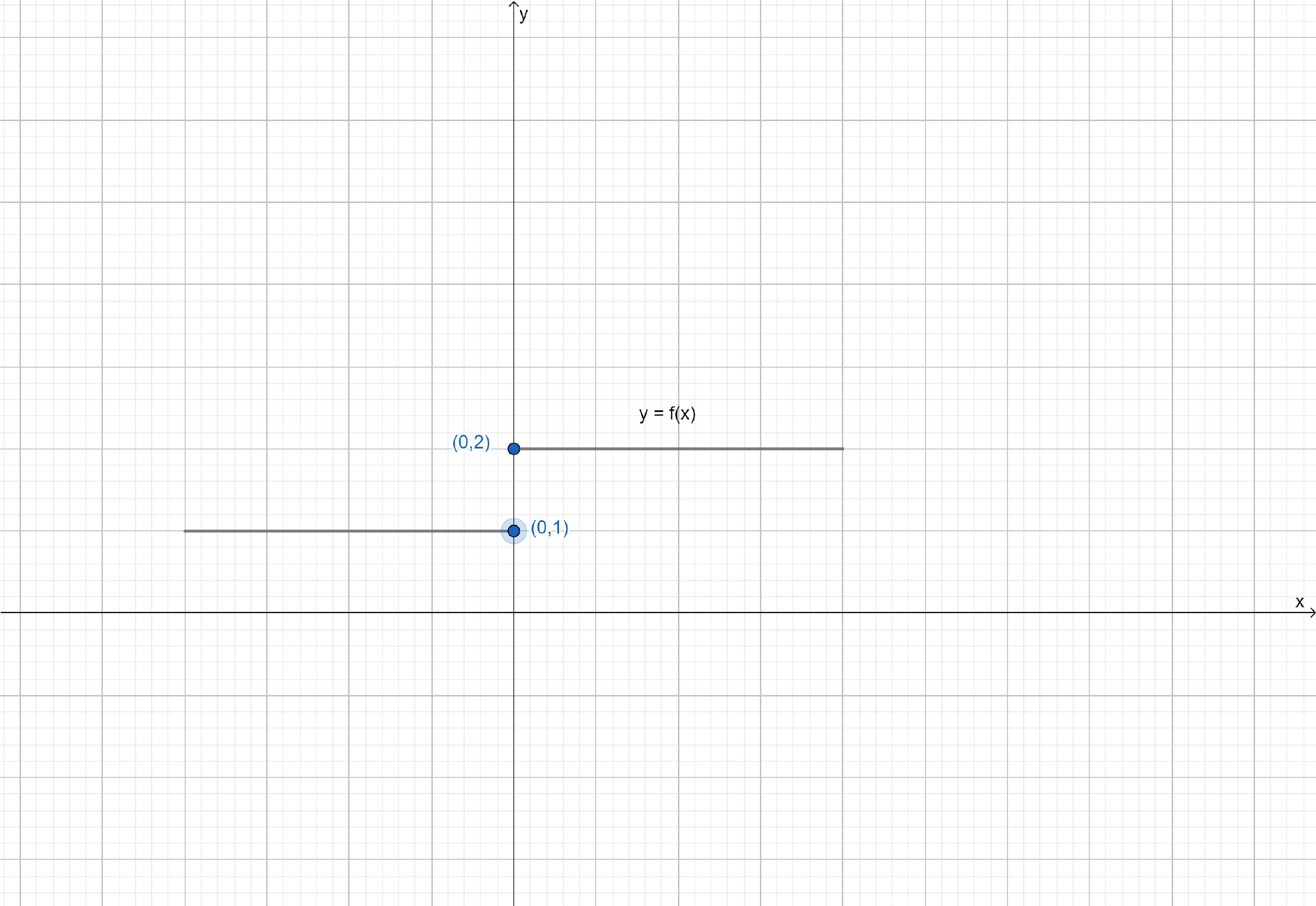
One can deduce from the graph that the value of the function at nearly points on $x$-axis remains close to each other except at $x = 0$. At the points near and to the left of $0$, i.e., at points like $- 0.1, - 0.01, - 0.001$, the value of the functions is $1$. At the points near and to the right of $0$, i.e., at points like $0.1,0.01,0.001$, the value of the function is $2$. Using the language of left and right hand limits, we may say that the left (respectively right) hand limit of $f$ at $0$ is $1$ (respectively $2$). In particular the left and right hand limits do not coincide. We also observe that the value of the function at $x = 0$ coincides with the left hand limit. Note that when we try to draw the graph, we cannot draw it one stroke, i.e., without lifting a pen from the plane of the paper, we cannot draw the graph of this function. In fact, we need to lift the pen when we come to $0$ from left. This is one instance of function being not continuous.