Question

How do you find the component form of v given its magnitude $1$ and the angle it makes with the positive $x$ -axis is $\theta = 45^\circ$ ?

Answer 1

Let us first assume a circle of radius $1$ , now draw a radius line at $45^\circ$ . Write the general form of any coordinates on a circle that is located at an angle $\theta$ . Since it is given that the vector is placed at $45^\circ$ , substitute the values and then represent the vectors in component form.

Complete step by step answer:
Now first let’s draw a circle of radius $1$ .
Then the equation of that circle would be ${x^2} + {y^2} = 1$
The general form of any coordinates on a circle in polar form is,
$(x,y) = (r\cos \theta ,r\sin \theta )$

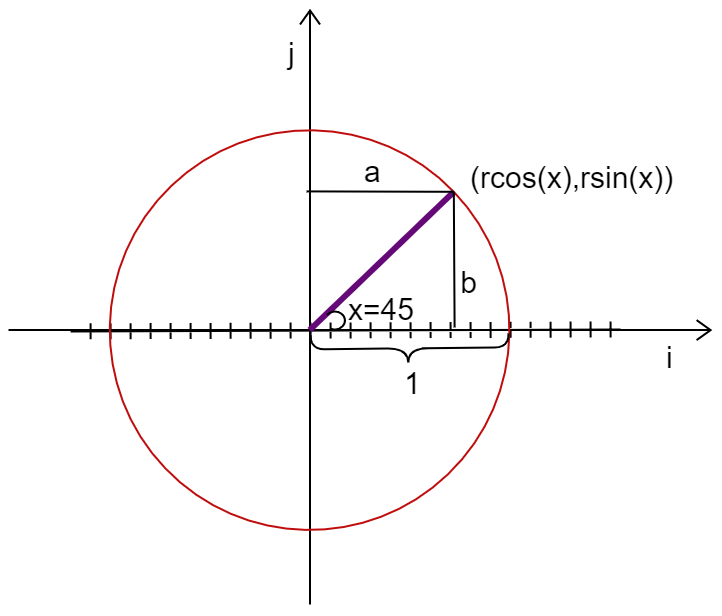
Since it is given that our vector is at an angle $45^\circ$ from the $x$ -axis,
$\tan 45^\circ = 1$
This also means that our vector is going to be in form of $a\hat i + b\hat j$ where $a = b$
We find the point on the circle which is at an angle $45^\circ$ from the $x$ -axis.
We find the point on the circle because it is given in the question that the magnitude of the vector is $1$ and here our circle is also of the radius $1$.
It is easier to find the point which lies on the circle and its component.
$\Rightarrow (r\cos 45^\circ ,r\sin 45^\circ )$
Since the radius is equal to $1$ , substitute the values of $r$ and the trigonometric values.
$\Rightarrow ((1)\cos 45^\circ ,(1)\sin 45^\circ )$
$\Rightarrow \left( {\dfrac{1}{{\sqrt 2 }},\dfrac{1}{{\sqrt 2 }}} \right)$
Let the representation of components in vector be of the form,
\Rightarrow v = \left( {\begin{array}{*{20}{c}} x \\\ y \end{array}} \right) The vector $v$ has $x,y\;$ as its components then,
$\Rightarrow \left| {|v|} \right| = \sqrt {{x^2} + {y^2}} = 1$
Which again comes to the equation of the circle, ${x^2} + {y^2} = 1$
Now we write the solution in component form.
\Rightarrow v = \left( {\begin{array}{*{20}{c}} {\dfrac{1}{{\sqrt 2 }}} \\\ {\dfrac{1}{{\sqrt 2 }}} \end{array}} \right)We can also prove our answer by substituting in this equation, $\left| {|v|} \right| = \sqrt {{x^2} + {y^2}} = 1$
$\Rightarrow \left| {|v|} \right| = \sqrt {{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^2} + {{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^2}}$
Now evaluate further to get,
$\Rightarrow \left| {|v|} \right| = \sqrt {\left( {\dfrac{1}{2}} \right) + \left( {\dfrac{1}{2}} \right)}$
We can rewrite this as,
$\Rightarrow \left| {|v|} \right| = \sqrt 1 = 1$

$\therefore$ The vector of magnitude $1$ making $45^\circ$ with $x$ -axis is $\dfrac{1}{{\sqrt 2 }}\hat i + \dfrac{1}{{\sqrt 2 }}\hat j$

Note: Whenever a vector component of any vector is asked to find out, we multiply the given magnitude with the unit vector in the same direction making the same angle. If the angle the vector makes is $45^\circ$ , then the magnitude of the constants in front of $i,j\;$ is going to be the same. If the vector $a\hat i + b\hat j$ makes the angle $45^\circ$ , then $a = b$ .