Question

How do you find the circumference of a circle circumscribed about a square with perimeter 40 in?

Answer 1

In this problem, we have to find the circumference of the circle. We are given the perimeter of the square, with which we can find the side of the square. By using the side of the square, we can use Pythagoras theorem to find the radius of the circle with which we can find the circumference of the circle by using the circumference of the circle formula.

Complete step by step solution:
We know that the given perimeter of the square is 40 in.
We can find the side of the given square whose perimeter is 40 in.
As all the sides of the square are equal, If the perimeter is 40, then each side is,
$\Rightarrow \dfrac{40}{4}=10$in.
Now we can assume the diagram as,

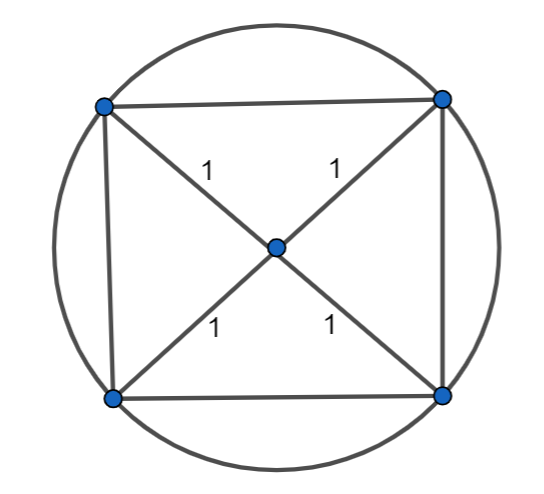
We can assume that, if the radius of the circle is 1 unit, then the side of the square by the Pythagoras theorem is
$\Rightarrow \sqrt{{{1}^{2}}+{{1}^{2}}}=\sqrt{2}$
We already know that the side of the square is 10, then the radius of the circle would be,
Radius of the circle = $\dfrac{10}{\sqrt{2}}$.
We know that the circumference of the circle = $2\pi r$.
$\Rightarrow 2\times \pi \times \dfrac{10}{\sqrt{2}}=\sqrt{2}\times \pi \times 10$
We know that the value of $\pi =3.14,\sqrt{2}=1.4142$.
We can substitute these values in the circumference formula, we get
The circumference of the circle = $3.14\times 10\times 1.4142=44.4285$.
Therefore, the circumference of the circle = $44.4285$in.

Note: Students make mistakes, while finding the sides of the square, which is used to find the radius of the circle. The length of sides can be found by dividing the perimeter to the number of sides. We should also know the Pythagoras theorem to find the other side of the square.