Question
Question: How do you find the centre, vertices, foci and eccentricity of \[9{{x}^{2}}+25{{y}^{2}}=225\]?...
How do you find the centre, vertices, foci and eccentricity of 9x2+25y2=225?
Solution
This question is from the topic of ellipse. In this question, we will first divide the term 225 to the both sides of the equation. After that, we will understand how to find centre, vertices, foci and eccentricity of ellipse from the general equation of ellipse. After that, we will know the general equation of ellipse. After that, we will find the centre, vertices, foci and eccentricity using the equation 9x2+25y2=225.
Complete step by step solution:
Let us solve this question.
In this question, it is asked to find the vertices, centre, foci and eccentricity of the equation of ellipse which is given in the question as 9x2+25y2=225
After dividing 225 to the both side of equation, we can write the equation 9x2+25y2=225 as
⇒2259x2+22525y2=225225
Now, let us understand the formula of the general equation of ellipse.
The equation is a2(x−h)2+b2(y−k)2=1 general equation of ellipse.
From the above equation of ellipse, we can say that
The centre of ellipse will be (h,k)
Foci of ellipse will be (h+c,k) and (h−c,k)
Vertices of ellipse will be (h+a,k) and (h−a,k)
Eccentricity of ellipse will be e=ac=aa2−b2
Now, we have equation of ellipse as
2259x2+22525y2=225225
As we know that, if we divide 225 by 9 then we get 25 and if we divide 225 by 25 then we get 9, so we can write the above equation as
⇒25x2+9y2=1
The above equation can also be written as
⇒52x2+32y2=1
The above equation can also be written as
⇒52(x−0)2+32(y−0)2=1
From the above ellipse equation, we can say that
a=5, b=3, h=0, and k=0
c=a2−b2=52−32=25−9=16=4
Now, we can see that
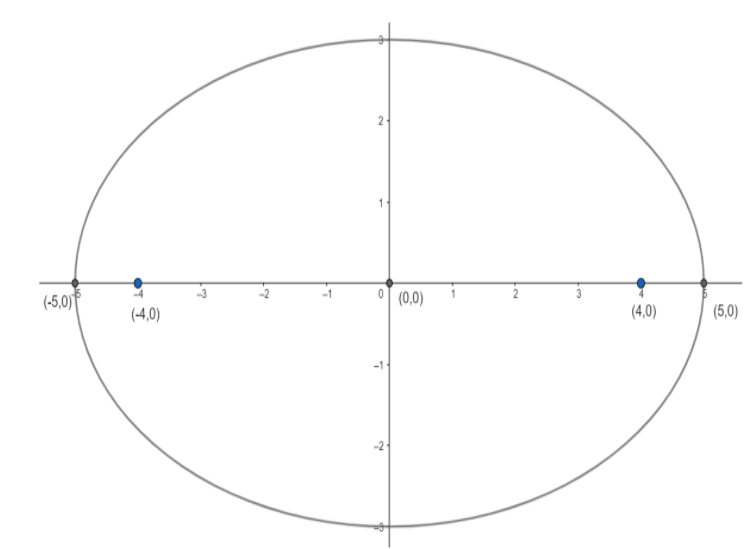
The centre is (0,0)
Foci are (4,0) and (-4,0)
Vertices are (5,0) and (-5,0)
Eccentricity is e=ac=54
Now, we have found the centre, eccentricity, vertices and foci.
We can take reference from the following figure.
Note: We should have a better knowledge in the topic of ellipse which is from the chapter coordinate geometry.
Remember that the general equation of ellipse is a2(x−h)2+b2(y−k)2=1
Always remember the square of some specific numbers like the square of 15 is 225, the square 0f 3 is 9 and the square of 5 is 25.
Remember of formula of eccentricity that is e=bc=bb2−a2
