Question

How do you find the centre, radius, x-intercept and y-intercept and graph of the circle: “ $x^2+y^2-2x-4y-4=0$ ”

Answer 1

Hint : For finding the centre and other values for a circle you need to know the general equation of the circle, and then comparing from the general equation you can directly have the required coordinates what you need, in the question. The general equation of circle is:
$\Rightarrow {\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$ Here “(h,k)” is centre of circle and “r” is radius of circle.

Complete step-by-step answer :
The given question is ${x^2} + {y^2} - 2x - 4y - 4 = 0$
Now we have to arrange this equation in the form of general equation so as on comparison we can directly get the centre coordinate, here we had to add and subtract “4” and “1” in the equation so to obtain the perfect squares of the variables and then we can compare the equation,on solving we get:

$$\Rightarrow {x^2} + {y^2} - 2x - 4y - 4 = 0 \\\ \Rightarrow {x^2} + {y^2} - 2x - 4y + (1 - 1) + (4 - 4) - 4 = 0\,(here\,4\,and\,1\,is\,added\,and\,subtracted\,to\,make\,the\,perfect\,square\,for\,the\,x\,and\,y\,coordinate) \\\ \Rightarrow {x^2} - 2x + 1 + {y^2} - 4y + 4 - 1 - 4 - 4 = 0 \\\ \Rightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} - 9 = 0 \\\ \Rightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9 \\\ \Rightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = {3^2} \;$$

Now we can compare both the equation that is our obtained equation and general equation of circle, on comparison we get:
$\Rightarrow (h,k) = (1,2)\,and\,radius\,r = 3$

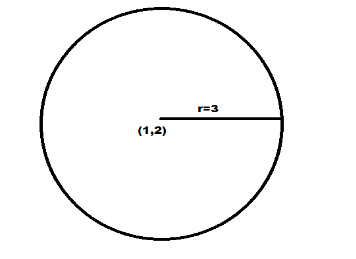
So, the correct answer is “ $\ (h,k) = (1,2)\,and\,radius\,r = 3$ ”.

Note : Circle is an ellipse whose major and minor axis are equal, but its general equation is very easy to learn and solve. To obtain the general equation you have to take a point on the circle and then from the centre of the circle to that point write the equation of length between two points which is equal to the radius of the circle.