Question

How do you find the centre-radius form of the equation of the circle having a diameter with endpoints $\left( -5,1 \right)$ and$\left( 11,13 \right)$?

Answer 1

From the question given, we have been asked to find the centre-radius form of the equation of the circle having a diameter with endpoints $\left( -5,1 \right)$ and$\left( 11,13 \right)$. First of all, to solve the given question, we have to know about the general form of the centre-radius form of the equation of the circle. General form of the centre-radius form of the equation of the circle is shown below: ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ where, $\left( a,b \right)$ is the centre of the circle and $r$ is the radius of the circle.

Complete step by step answer:
From the question it has been given that $\left( -5,1 \right)$ and $\left( 11,13 \right)$ are the endpoints of the diameter. So, the centre of the circle is at the midpoint of the endpoints of diameter.
General form of the centre-radius form of the equation of the circle is given as ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ where, $\left( a,b \right)$ is the centre of the circle and $r$ is the radius of the circle.
Therefore, centre of the circle is:
$\Rightarrow \left( \dfrac{-5+11}{2},\dfrac{1+13}{2} \right)$
$\Rightarrow \left( \dfrac{6}{2},\dfrac{14}{2} \right)$
$\Rightarrow \left( 3,7 \right)$
Therefore, the centre of the circle is $\left( 3,7 \right)$.
Therefore, the centre of the given circle is $\left( a,b \right)=\left( 3,7 \right)$.
We know that radius is the distance from the centre of the circle to any one of the endpoints of the diameter.
Therefore, the radius for this question will be the distance from the centre of the circle $\left( 3,7 \right)$ to any one of the endpoints of the diameter (I will take $\left( 11,13 \right)$).

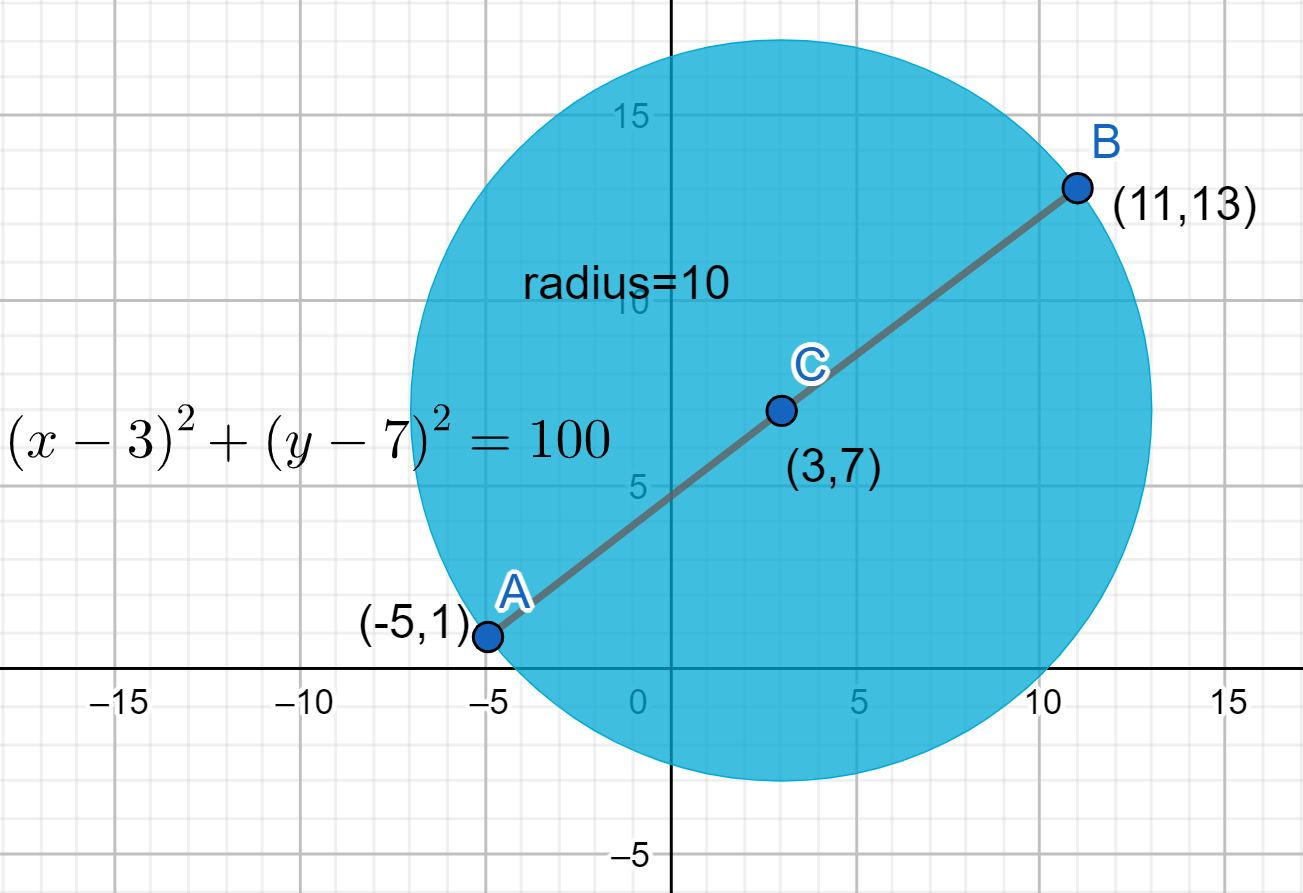
Radius of the circle can be given by using the concept that says that the radius is the distance between the endpoint and the centre of a circle,
$\Rightarrow r=\sqrt{{{\left( 11-3 \right)}^{2}}+{{\left( 13-7 \right)}^{2}}}$
$\Rightarrow r=\sqrt{{{8}^{2}}+{{6}^{2}}}$
$\Rightarrow r=\sqrt{64+36}$
$\Rightarrow r=\sqrt{100}$
$\Rightarrow r=10$
By substituting the values we got in the general form of the centre-radius form of the circle we get,
${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$
$\Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-7 \right)}^{2}}={{10}^{2}}$
Therefore, the above equation is the centre-radius form for the given question.

Note: We should be well known about the general form of the centre-radius form of the equation of the circle. Also, we should be very careful while doing the calculation part. Also, we should be very careful while finding the centre of the circle using the endpoints of the diameter and should be very careful while finding the radius of the circle by using the distance formulae. Distance formulae for finding the distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as $\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$