Question

How do you find the centre of the circle with equation ${{\left( x-3 \right)}^{2}}+{{\left( y+4 \right)}^{2}}=25$?

Answer 1

In this problem, we have to find the centre of the given equation of the circle. To find the centre, we can compare the given equation with the general equation of the circle to find the value of h and k, which are the points of centre. We will have the points of centre h, k in the general equation, so that we can just compare it with the given equation to find the centre value.

Complete step by step solution:
We know that the given equation of the circle is,
${{\left( x-3 \right)}^{2}}+{{\left( y+4 \right)}^{2}}=25$ …….. (1)
We know that the general equation of the circle is,
${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$ ……… (2)
We can now compare the equation (1) and the equation (2), we get
h = 3, k = -4.
Therefore, the centre of the given equation of the circle ${{\left( x-3 \right)}^{2}}+{{\left( y+4 \right)}^{2}}=25$ is $\left( 3,-4 \right)$.
We can now draw the graph,

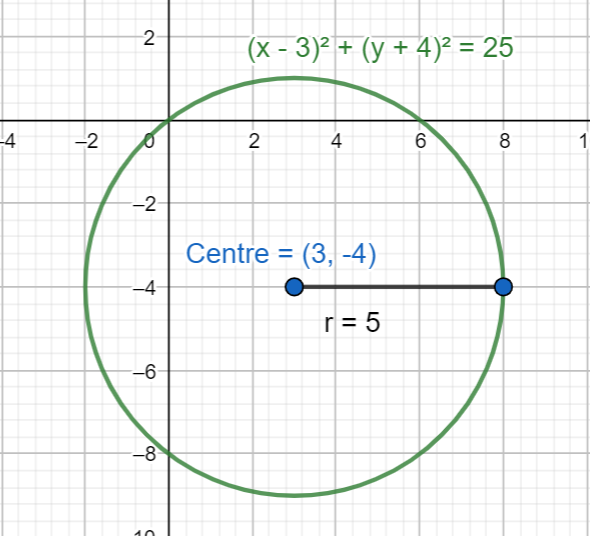
Note: Students make mistakes in the positive and the negative sign part while comparing the given equation of the circle and the general equation of the circle. We should remember that the centre points are subtracted from the axis and added up. We can now substitute the resulted points in the general equation to get the given equation to be correct.
The resulting points are h = 3, k = -4.
We can substitute in general form, we get

& \Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-\left( -4 \right) \right)}^{2}}=25 \\\ & \Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y+4 \right)}^{2}}=25 \\\ \end{aligned}$$ Therefore, the resulting centre point $$\left( 3,-4 \right)$$ is correct.