Solveeit Logo
Login

Question

Question: How do you find the centre of the circle that is circumscribed about the triangle with the vertices ...

How do you find the centre of the circle that is circumscribed about the triangle with the vertices (0,-2), (7,-3) and (8,-2)?

Explanation

Solution

This question belongs to the topic of circle which belongs to the topic of coordinate geometry. We will first find the perpendicular bisectors of the lines which are the sides of the triangle. We will use the formula of the perpendicular bisector of a line to find the equation of line. We will see the figure and understand this question and then find the centre of the circle.

Complete step by step solution:
Let us solve this question.
In this question, we have asked to find the centre of the circle that is circumscribed about the triangle with the vertices (0,-2), (7,-3) and (8,-2). Or, we can say the points are given as the three vertices of a triangle and also these points lie on the circle. So, we have to find the centre of the circle using these points.
Let us understand this from the following figure.

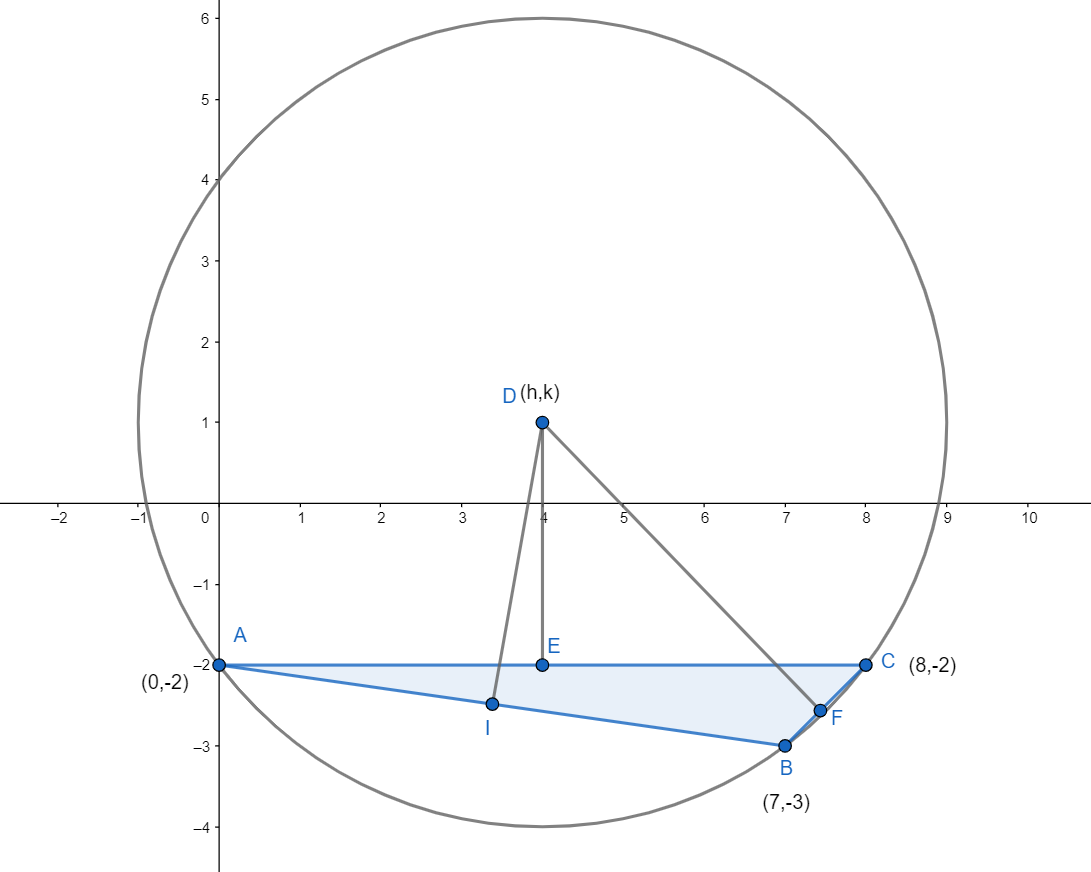
As we can see that the sides of the triangle ABC are the chords of the circle and we know that the perpendicular bisector of the chord of the circle meets at the centre of the circle. And, in the figure we can see that ID, ED, and FD are the perpendicular bisector of the chords AB, AC, and BC respectively.
As we know that if a line is having the points (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and (x2,y2)\left( {{x}_{2}},{{y}_{2}} \right), then the line of perpendicular bisector of the given line having those points will be (y−y1+y22)=−(x2−x1y2−y1)(x−x1+x22)\left( y-\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)=-\left( \dfrac{{{x}_{2}}-{{x}_{1}}}{{{y}_{2}}-{{y}_{1}}} \right)\left( x-\dfrac{{{x}_{1}}+{{x}_{2}}}{2} \right)
Now, we can say from the above figure that the points on the line AC are (0,-2) and (8,-2), then the perpendicular bisector of the line AC that is ED will be
(y−−2−22)=−(8−0−2−(−2))(x−0+82)\left( y-\dfrac{-2-2}{2} \right)=-\left( \dfrac{8-0}{-2-\left( -2 \right)} \right)\left( x-\dfrac{0+8}{2} \right)
The above equation can also be written as
⇒(y−(−2))=−(8−2+2)(x−4)\Rightarrow \left( y-\left( -2 \right) \right)=-\left( \dfrac{8}{-2+2} \right)\left( x-4 \right)
The above equation can also be written as
⇒(y+2)=−(80)(x−4)\Rightarrow \left( y+2 \right)=-\left( \dfrac{8}{0} \right)\left( x-4 \right)
The above equation can also be written as
⇒0×(y+2)=−(8)(x−4)\Rightarrow 0\times \left( y+2 \right)=-\left( 8 \right)\left( x-4 \right)
The above equation can also be written as
⇒0=−(8)(x−4)\Rightarrow 0=-\left( 8 \right)\left( x-4 \right)
⇒0−(8)=(x−4)\Rightarrow \dfrac{0}{-\left( 8 \right)}=\left( x-4 \right)
⇒0=(x−4)\Rightarrow 0=\left( x-4 \right)
⇒x=4\Rightarrow x=4
Hence, we get that the equation of line ED is x=4x=4.
Similarly, the line AB has points (0,-2) and (7,-3). So, the equation of its perpendicular bisector that is the equation of ID using the formula (y−y1+y22)=−(x2−x1y2−y1)(x−x1+x22)\left( y-\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)=-\left( \dfrac{{{x}_{2}}-{{x}_{1}}}{{{y}_{2}}-{{y}_{1}}} \right)\left( x-\dfrac{{{x}_{1}}+{{x}_{2}}}{2} \right) will be
(y−−2+(−3)2)=−(7−0−3−(−2))(x−0+72)\left( y-\dfrac{-2+\left( -3 \right)}{2} \right)=-\left( \dfrac{7-0}{-3-\left( -2 \right)} \right)\left( x-\dfrac{0+7}{2} \right)
The above equation can also be written as
⇒(y−−2−32)=−(7−3+2)(x−72)\Rightarrow \left( y-\dfrac{-2-3}{2} \right)=-\left( \dfrac{7}{-3+2} \right)\left( x-\dfrac{7}{2} \right)
⇒(y−−52)=−(7−1)(x−72)\Rightarrow \left( y-\dfrac{-5}{2} \right)=-\left( \dfrac{7}{-1} \right)\left( x-\dfrac{7}{2} \right)
⇒(y+52)=7(x−72)\Rightarrow \left( y+\dfrac{5}{2} \right)=7\left( x-\dfrac{7}{2} \right)
⇒y+52=7x−7×72\Rightarrow y+\dfrac{5}{2}=7x-7\times \dfrac{7}{2}
⇒y+52=7x−492\Rightarrow y+\dfrac{5}{2}=7x-\dfrac{49}{2}
⇒y=7x−492−52\Rightarrow y=7x-\dfrac{49}{2}-\dfrac{5}{2}
⇒y=7x−492−52=7x−(492+52)=7x−(49+52)=7x−(542)\Rightarrow y=7x-\dfrac{49}{2}-\dfrac{5}{2}=7x-\left( \dfrac{49}{2}+\dfrac{5}{2} \right)=7x-\left( \dfrac{49+5}{2} \right)=7x-\left( \dfrac{54}{2} \right)
⇒y=7x−27\Rightarrow y=7x-27
Now, we get that the equation of line ID is y=7x−27y=7x-27.
Now, we can say that the lines ED (or, x=4) and ID (or, y=7x−27y=7x-27) are meeting at a point that is centre. So, using these lines we will find the centre.
Now, putting the value of x=4 in the equation y=7x−27y=7x-27, we get
y=7×4−27=28−27=1y=7\times 4-27=28-27=1
Hence, we get the points as x=4 and y=1. So, we can say that the centre of circle will be (4,1)
Note: We should have a better knowledge in the topic of circle. We should know how to find the perpendicular bisector of the line. Let us understand this from the following:

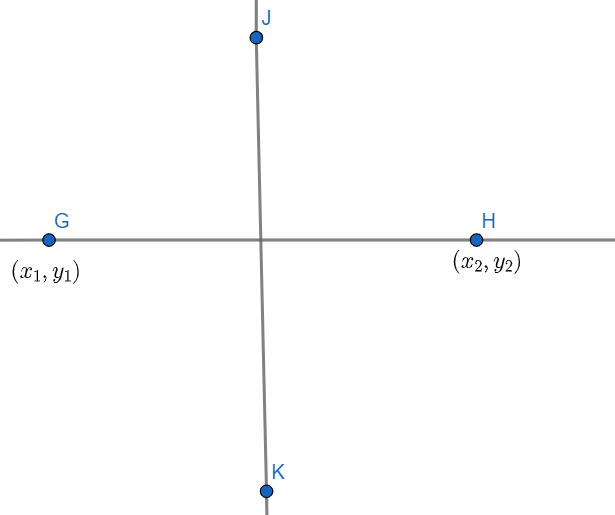
Suppose, the two points are given on the line GH that are G(x1,y1)G\left( {{x}_{1}},{{y}_{1}} \right) and H(x2,y2)H\left( {{x}_{2}},{{y}_{2}} \right) & the line JK is perpendicular bisector of the line GH. So, we can say that the formula for line JK will be (y−y1+y22)=−(x2−x1y2−y1)(x−x1+x22)\left( y-\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)=-\left( \dfrac{{{x}_{2}}-{{x}_{1}}}{{{y}_{2}}-{{y}_{1}}} \right)\left( x-\dfrac{{{x}_{1}}+{{x}_{2}}}{2} \right)