Question

How do you find the centre of ${{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=50$?

Answer 1

This question is from the topic of circle which belongs to the chapter coordinate geometry. We will know about the general equation of the circle. After that, we will understand how to find the centre from the general equation of the circle. After that, we will find the centre of circle of the equation ${{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=50$ which is given in the question.

Complete step by step solution:
Let us solve this question.
In this question, it is asked us to find the centre of ${{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=50$. We can see that this equation is the equation of a circle.
Let us first understand how to find the centre of a circle from the general equation of circle.
The general equation of circle in the form of equation is written as
${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$
Now, from here we can say that
The centre of circle is at (h,k)
So, on comparing the general equation of circle from the given equation of circle that is ${{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=50$, we can say that the centre will be (-2,3)
Hence, we have found the centre of the equation ${{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=50$. The centre of the equation ${{\left( x+2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=50$ is (-2,3)
We can take reference from the following figure.

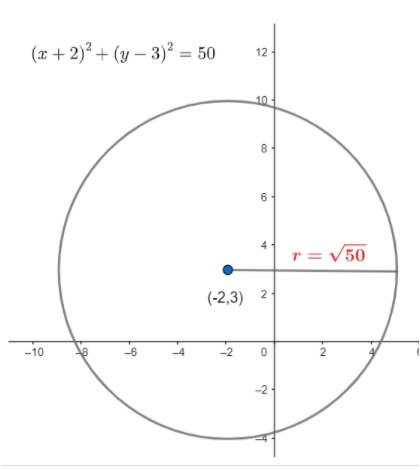
Note: As we can see that this question is from the topic of circle which belongs to the chapter of coordinate geometry, so we should have a better knowledge in that topic. We should always remember the general equation of a circle. The general equation of circle is ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$ and the centre of the circle of this equation is (h,k) and radius of circle of this equation is r.