Question

How do you find the centre (h,k) and the radius r of the circle with the given equation ${{x}^{2}}+{{y}^{2}}-18x+18y=-137$?

Answer 1

This question is from the topic of circle of the chapter coordinate geometry. In solving this question, we will first solve the equation ${{x}^{2}}+{{y}^{2}}-18x+18y=-137$ and make it in the form of the general equation of circle by completing the square. After that, we will understand the general equation of the circle and find the centre and radius from the given equation of the circle.

Complete step by step solution:
Let us solve this question.
In this question, we have asked to find the centre (h,k) and radius r of the circle of given equation ${{x}^{2}}+{{y}^{2}}-18x+18y=-137$. We will find a general equation of the circle.
The given equation is
${{x}^{2}}+{{y}^{2}}-18x+18y=-137$
The above equation can also be written as
$\Rightarrow {{x}^{2}}+{{y}^{2}}-18x+18y+137=0$
The above equation can also be written as
$\Rightarrow {{x}^{2}}+18x+{{y}^{2}}-18y+137=0$
Now, we will make a perfect square of the term x and y.
The above equation can also be written as
$\Rightarrow {{x}^{2}}+2\times 9\times x+{{y}^{2}}-2\times 9\times y+137=0$
Now, adding the square of 9 two times on both the side of equation, we get
$\Rightarrow {{x}^{2}}+2\times 9\times x+{{9}^{2}}+{{y}^{2}}-2\times 9\times y+{{9}^{2}}+137={{9}^{2}}+{{9}^{2}}$
The above equation can also be written as
$\Rightarrow {{x}^{2}}+2\times 9\times x+{{9}^{2}}+{{y}^{2}}-2\times 9\times y+{{9}^{2}}=81+81-137$
Now, we can see that on the left side of the equation the first 3 terms is square of (x+9) and last three terms is the square of (y-9). So, we can write the above equation as
$\Rightarrow {{\left( x+9 \right)}^{2}}+{{\left( y-9 \right)}^{2}}=167-137$
$\Rightarrow {{\left( x+9 \right)}^{2}}+{{\left( y-9 \right)}^{2}}=25$
The above equation can also be written as
$\Rightarrow {{\left( x+9 \right)}^{2}}+{{\left( y-9 \right)}^{2}}={{5}^{2}}$
Now, we know that general equation of circle is ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$, and the radius of circle is r and the centre of the circle is (h,k).
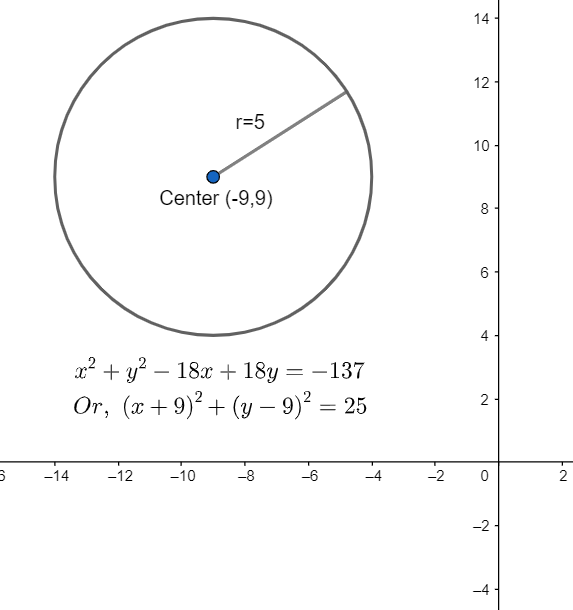
So, we can say from the equation ${{\left( x+9 \right)}^{2}}+{{\left( y-9 \right)}^{2}}={{5}^{2}}$ that the centre is (-9,9) and the radius of circle is 5 units.
Hence, the centre of the equation ${{x}^{2}}+{{y}^{2}}-18x+18y=-137$ is (-9,9) and the radius of the equation ${{x}^{2}}+{{y}^{2}}-18x+18y=-137$ is 5 units.
We can take reference from the following figure.

Note: We should have a better knowledge in the topic of circle. We should always remember the formulas of radius and centre of circle. Remember that if the general equation of circle is ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$, then the centre of the circle of this equation is (h,k) and the radius of circle of this equation is r. We should know how to make a perfect square. The steps for making a perfect square by completing the square are in the following:
Suppose we have a general equation $a{{x}^{2}}+bx+c=0$

1. first, divide all the terms by ‘a’ (the coefficient of ${{x}^{2}}$)
   ${{x}^{2}}+\dfrac{b}{a}x+\dfrac{c}{a}=0$
2. complete the square of the equation and balance this by adding the square of $\dfrac{b}{2a}$ to the both sides of the equation.
   ${{x}^{2}}+2\times \dfrac{b}{2a}x+{{\left( \dfrac{b}{2a} \right)}^{2}}+\dfrac{c}{a}={{\left( \dfrac{b}{2a} \right)}^{2}}$
3. after that, we will write the in the form of perfect square
   ${{\left( x+\dfrac{b}{2a} \right)}^{2}}+\dfrac{c}{a}={{\left( \dfrac{b}{2a} \right)}^{2}}$