Question

How do you find the center, foci and vertices of $16{{x}^{2}}+25{{y}^{2}}-32x+50y+16=0$ ?

Answer 1

To find the center, foci and vertices of $16{{x}^{2}}+25{{y}^{2}}-32x+50y+16=0$ , we have to rearrange the equation in the form $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$ , where $\left( h,k \right)$ is the centre, a is the major axis and b is the minor axis. We will determine whether the ellipse is horizontal or vertical by checking whether $a> b$ or $a< b$ . The former leads to horizontal ellipse while the latter forms a vertical ellipse. The vertices are given by $\left( h\pm a,k \right)$ and foci are given by $\left( h\pm c,k \right)$ . We can find c by using the equation ${{c}^{2}}={{a}^{2}}-{{b}^{2}}$ .

Complete step by step solution:
We have to find the center, foci and vertices of $16{{x}^{2}}+25{{y}^{2}}-32x+50y+16=0$ . We can see that x and y are squared and their coefficients are positive and different. Hence, the given equation is that of an ellipse. We know that equation of an ellipse with centre $\left( h,k \right)$ , major axis a and minor axis b, is given by
$\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1...\left( i \right)$ .
Now, we have to convert the given equation in the form of equation (i). Let us rearrange the given equation as shown below.
$\begin{aligned} & 16{{x}^{2}}+25{{y}^{2}}-32x+50y+16=0 \\\ & \Rightarrow 16{{x}^{2}}-32x+16+25{{y}^{2}}+50y=0 \\\ \end{aligned}$
Let us take the common factors outside.
$\Rightarrow 16\left( {{x}^{2}}-2x+1 \right)+25\left( {{y}^{2}}+2y \right)=0$
We need to add a term in the second bracket so that we will get an equation of the form $\left( {{a}^{2}}+2ab+{{b}^{2}} \right)$ . For this, we will take the coefficient of y and divide it by 2 and then take its square, that is, ${{\left( \dfrac{2}{2} \right)}^{2}}=1$ . Hence, the above equation can be written as
$\begin{aligned} & \Rightarrow 16\left( {{x}^{2}}-2x+1 \right)+25\left( {{y}^{2}}+2y+1-1 \right)=0 \\\ & \Rightarrow 16\left( {{x}^{2}}-2x+1 \right)+25\left( {{y}^{2}}+2y+1 \right)-25=0 \\\ \end{aligned}$
We know that ${{\left( a+b \right)}^{2}}=\left( {{a}^{2}}+2ab+{{b}^{2}} \right)$ and ${{\left( a-b \right)}^{2}}=\left( {{a}^{2}}-2ab+{{b}^{2}} \right)$ . Hence, we can write the above equation as
$\Rightarrow 16{{\left( x-1 \right)}^{2}}+25{{\left( y+1 \right)}^{2}}-25=0$
Let us take the third term to RHS.
$\Rightarrow 16{{\left( x-1 \right)}^{2}}+25{{\left( y+1 \right)}^{2}}=25$
We have to make the RHS as 1. SO let us divide the LHS and RHS by 25.
$\begin{aligned} & \Rightarrow \dfrac{16}{25}{{\left( x-1 \right)}^{2}}+\dfrac{25}{25}{{\left( y+1 \right)}^{2}}=\dfrac{25}{25} \\\ & \Rightarrow \dfrac{16}{25}{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}=1 \\\ \end{aligned}$
We can rewrite the equation as
$\Rightarrow \dfrac{{{\left( x-1 \right)}^{2}}}{\dfrac{25}{16}}+\dfrac{{{\left( y+1 \right)}^{2}}}{1}=1$
We can see that the above equation is of the form of equation (i). Hence, we can see that the centre of the given ellipse is $\left( 1,-1 \right)$ . Let us find a and b.
$\begin{aligned} & {{a}^{2}}=\dfrac{25}{16} \\\ & \Rightarrow a=\sqrt{\dfrac{25}{16}}=\dfrac{5}{4} \\\ \end{aligned}$
$\begin{aligned} & {{b}^{2}}=1 \\\ & \Rightarrow b=1 \\\ \end{aligned}$
We can see that $a>b$ . Hence, the ellipse is horizontal.
We know that for a horizontal ellipse, vertices are given by $\left( h\pm a,k \right)$ . Hence, the vertices of the given ellipse are:
$\begin{aligned} & \left( 1\pm \dfrac{5}{4},-1 \right) \\\ & \Rightarrow \left( 1+\dfrac{5}{4},-1 \right),\left( 1-\dfrac{5}{4},-1 \right) \\\ & \Rightarrow \left( \dfrac{9}{4},-1 \right),\left( -\dfrac{1}{4},-1 \right) \\\ \end{aligned}$
To find the foci, we need to find the distance of the foci from the centre. We know that ${{c}^{2}}={{a}^{2}}-{{b}^{2}}$ . Let us substitute the values in this equation.
$\begin{aligned} & \Rightarrow {{c}^{2}}=\dfrac{25}{16}-1 \\\ & \Rightarrow {{c}^{2}}=\dfrac{25-16}{16} \\\ & \Rightarrow {{c}^{2}}=\dfrac{9}{16} \\\ \end{aligned}$
Let us take the square root.
$\Rightarrow c=\sqrt{\dfrac{9}{16}}=\dfrac{3}{4}$
We know that foci of horizontal ellipse are at $\left( h\pm c,k \right)$ . Hence, the foci of the give ellipse are at
$\begin{aligned} & \left( 1\pm \dfrac{3}{4},-1 \right) \\\ & =\left( 1+\dfrac{3}{4},-1 \right),\left( 1-\dfrac{3}{4},-1 \right) \\\ & =\left( \dfrac{7}{4},-1 \right),\left( \dfrac{1}{4},-1 \right) \\\ \end{aligned}$
Hence, the centre of the given ellipse is at $\left( 1,-1 \right)$ , vertices are at $\left( \dfrac{9}{4},-1 \right),\left( -\dfrac{1}{4},-1 \right)$ and foci are at $\left( \dfrac{7}{4},-1 \right),\left( \dfrac{1}{4},-1 \right)$ .
The graph below represents the given ellipse.

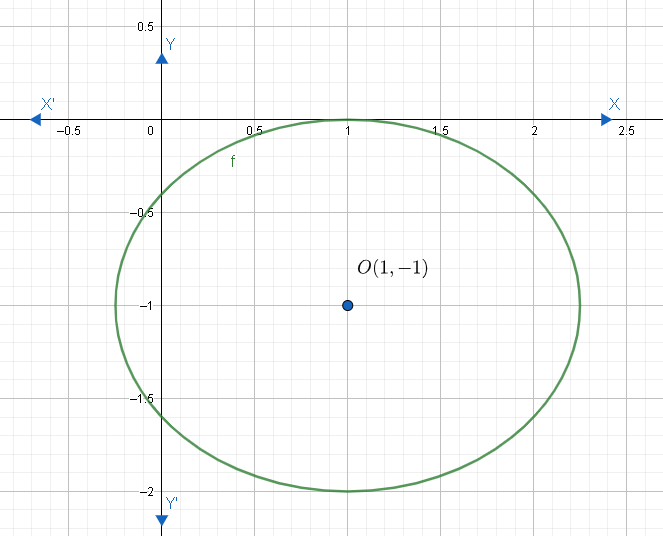
Note: When the given equation has x and y are squared and their coefficients are positive and different, then we can say that the given equation is an ellipse. If x and y are squared and their coefficients are the same including the sign, then we can say that the equation is of a circle. When either x or y is squared but not both, then we can confirm that the given equation is of a parabola. We can say that the given equation is of a hyperbola when x and y are both squared, and exactly one of the coefficients is negative and exactly one of the coefficients is positive. In case of an ellipse, if the major axis is less than the minor axis $a< b$ , then the ellipse will be vertical. For a vertical ellipse, we can write the vertices as $\left( h,k\pm a \right)$ and foci as $\left( h,k\pm c \right)$ .