Question

How do you find the center and radius of the circle ${{x}^{2}}+{{y}^{2}}-10x+6y+18=0$?

Answer 1

The general form of the equation of circle is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$. Here, we should note that the equation should not have a $xy$ term in it. We can find the values of the coefficients; we need to compare the given equation with the general form of the equation of the circle. To find the coordinates of the center of the circle and the radius using the values of the coefficient of the equation. The radius of the circle is $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.The coordinate of the center of circle are $\left( -g,-f \right)$.

Complete step by step solution:
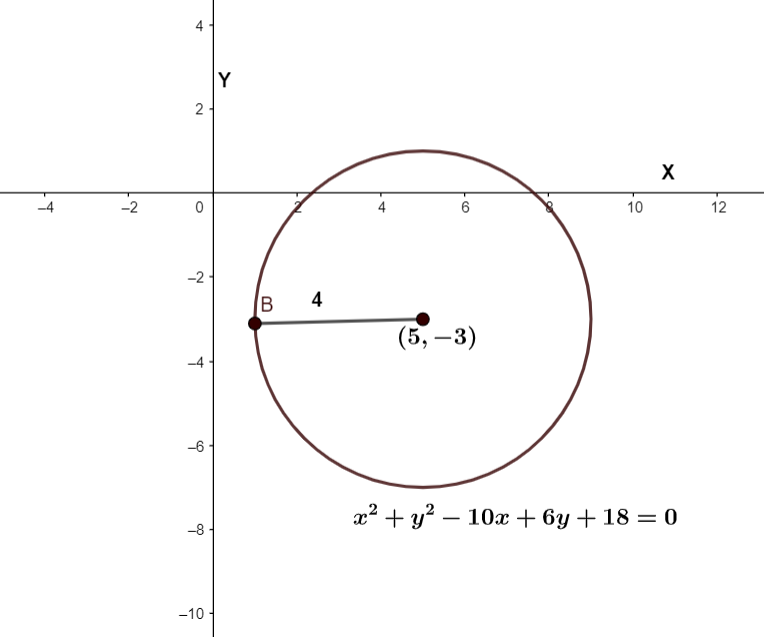
We are given the equation of the circle ${{x}^{2}}+{{y}^{2}}-10x+6y+18=0$. We need to find its center and radius. Comparing the given equation with the general form of the equation of the circle. We get the values of g, f, and c as $-5,3\And 18$ respectively. We know that for a circle represented by the general form of the equation, the X and Y coordinates of the center are $-g,-f$ respectively. Thus, for the given circle, by substituting the values of g and f, we get the coordinates of the center as $\left( -(-5),-3 \right)$. Simplifying this, we get center coordinates $\left( 5,-3 \right)$.
The radius of circle is $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$, substituting the values of g, f and c, we get radius as $\sqrt{{{5}^{2}}+{{\left( -3 \right)}^{2}}-18}=4$.
We can graph the circle as follows,

Note: While using the general equation of circle, one must be aware that the coefficients of $x\And y$ are not g and f but are $2g\And 2f$. As it is possible to make calculation mistakes while finding the values of coefficients for these. So, to find the value of g and f, divide the coefficients of $x\And y$ by 2.