Question

How do you find the center and radius of ${{\left( x-5 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=25$?

Answer 1

The equation of a circle in center radius form is ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. Here, a and b are the X-coordinate and Y-coordinate of the center. Thus, the coordinates of the center will be $\left( a,b \right)$. Also, r is the radius of the circle. So, using this form of equation, we can find the center and radius of the given circle.

Complete step by step solution:
We are given the equation of the circle as ${{\left( x-5 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=25$. We can see that this equation is of the form of ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ which is called center radius form of the equation of circle. Comparing this form, we can find the values of a, b and r for the given equation.
Thus, we get the values of $a,b,{{r}^{2}}$ as $5,-3,25$.
We know that the coordinates of the center of the circle represented by the center radius form are $\left( a,b \right)$. Substituting the values for a and b, we get $\left( 5,-3 \right)$.
Now, we need to find the radius. We already know that ${{r}^{2}}=25$. Here, r is the radius of the circle. Taking the square root of the given equation, we get $r=\sqrt{25}$. We know that the square root of 25 is 5. Hence, using this value, we get $r=5$.
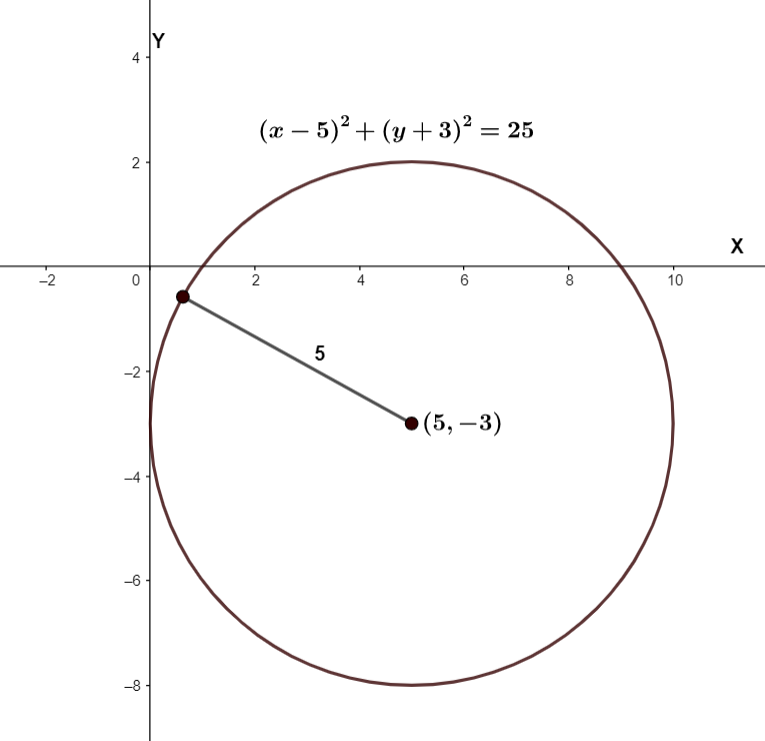
Hence, the coordinates of the center of the circle are $\left( 5,-3 \right)$, and the radius of the circle is 5.
We can also plot the graph of the circle as,

Note: To solve these types of questions, one should know how to find components of a conic using its equation. The different conics we should be familiar with are straight line, ellipse, hyperbola, etc. We can also use the general form of the equation of a circle to solve this problem, but it will require more calculations.