Solveeit Logo
Login

Question

Question: How do you find the center and radius of a circle using a polynomial \({{x}^{2}}+{{y}^{2}}-6x+10y+9=...

How do you find the center and radius of a circle using a polynomial x2+y2−6x+10y+9=0{{x}^{2}}+{{y}^{2}}-6x+10y+9=0?

Explanation

Solution

Convert the given polynomial to the standard form of circle (x−h)2+(y−k)2=(r)2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}}by completing square method. In completing the square method try to get three square terms of ‘x’, ‘y’ and constant. Then find the center and the radius by comparing the obtained expression with the general equation of the circle.

Complete step by step solution:
The standard form of general equation of circle is(x−h)2+(y−k)2=(r)2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}} where (h, k) is the center and ‘r’ is the radius.
The expression we have x2+y2−6x+10y+9=0{{x}^{2}}+{{y}^{2}}-6x+10y+9=0
We can convert the given equation to the standard form by completing the square method. For that we have to convert the whole expression to three square terms, one of ‘x’, one of ‘y’ and one of constant.
x2+y2−6x+10y+9=0 ⇒(x)2−2⋅x⋅3+(3)2−(3)2+(y)2+2⋅y⋅5+(5)2−(5)2+9=0 ⇒(x−3)2+(y+5)2−9−25+9=0 ⇒(x−3)2+(y+5)2=0+25 ⇒(x−3)2+(y−(−5))2=(5)2 \begin{aligned} & {{x}^{2}}+{{y}^{2}}-6x+10y+9=0 \\\ & \Rightarrow {{\left( x \right)}^{2}}-2\cdot x\cdot 3+{{\left( 3 \right)}^{2}}-{{\left( 3 \right)}^{2}}+{{\left( y \right)}^{2}}+2\cdot y\cdot 5+{{\left( 5 \right)}^{2}}-{{\left( 5 \right)}^{2}}+9=0 \\\ & \Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y+5 \right)}^{2}}-9-25+9=0 \\\ & \Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y+5 \right)}^{2}}=0+25 \\\ & \Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-\left( -5 \right) \right)}^{2}}={{\left( 5 \right)}^{2}} \\\ \end{aligned}
Now it is in the required form.
Comparing the above equation with the general equation of circle, we get
h=3, k=−5-5 and r=5
Hence, the center of the given circle is (3, −5-5) and radius is ‘5’.
It can be graphed as

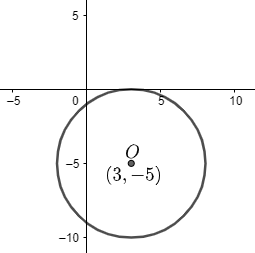
This is the required solution of the given question.
Note: A second degree heterogeneous equation ax2+2hxy+by2+2gx+2fy+c=0a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 may represent a conic if abc+2fgh−af2−bg2−ch2≠0abc+2fgh-a{{f}^{2}}-b{{g}^{2}}-c{{h}^{2}}\ne 0. For circle a=b and h=0, so the equation of circle becomes x2+y2+2gx+2fy+c=0{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0. In standard form it can be written as (x−h)2+(y−k)2=(r)2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}} where ‘h’ and ‘k’ represents the ‘x’ and ‘y’ offset from the origin respectively.