Solveeit Logo
Login

Question

Question: How do you find the center and radius for \(5{{x}^{2}}+5{{y}^{2}}+10x-30y+49=0\)?...

How do you find the center and radius for 5x2+5y2+10x−30y+49=05{{x}^{2}}+5{{y}^{2}}+10x-30y+49=0?

Explanation

Solution

Divide the given equation by ‘5’ to reduce the coefficient of ‘x2{{x}^{2}}’ and ‘y2{{y}^{2}}’. Then convert it to the standard form of circle i.e. (x−h)2+(y−k)2=(r)2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}} by completing square method. Compare the modified equation to the standard form of circle to get the center and the radius.

Complete step by step solution:
The equation of circle of the form x2+y2+2gx+2fy+c=0{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 can be converted to the standard form of circle i.e. (x−h)2+(y−k)2=(r)2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}} by completing square method. For that we have to convert the whole equation to three square terms, one of ‘x’, one of ‘y’ and one of constant.
The expression we have 5x2+5y2+10x−30y+49=05{{x}^{2}}+5{{y}^{2}}+10x-30y+49=0
First we have to reduce the coefficient of ‘x’ and ‘y’.
So, dividing by ‘5’ throughout the equation, we get
⇒5x2+5y2+10x−30y+495=05 ⇒x2+y2+2x−6y+495=0 ⇒(x)2+2⋅x⋅1+(1)2−(1)2+(y)2−2⋅y⋅3+(3)2−(3)2+495=0 ⇒(x+1)2+(y−3)2−1−9+495=0 ⇒(x+1)2+(y−3)2=10−495 ⇒(x+1)2+(y−3)2=50−495 ⇒(x+1)2+(y−3)2=15 ⇒(x−(−1))2+(y−3)2=(15)2 \begin{aligned} & \Rightarrow \dfrac{5{{x}^{2}}+5{{y}^{2}}+10x-30y+49}{5}=\dfrac{0}{5} \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}+2x-6y+\dfrac{49}{5}=0 \\\ & \Rightarrow {{\left( x \right)}^{2}}+2\cdot x\cdot 1+{{\left( 1 \right)}^{2}}-{{\left( 1 \right)}^{2}}+{{\left( y \right)}^{2}}-2\cdot y\cdot 3+{{\left( 3 \right)}^{2}}-{{\left( 3 \right)}^{2}}+\dfrac{49}{5}=0 \\\ & \Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}-1-9+\dfrac{49}{5}=0 \\\ & \Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=10-\dfrac{49}{5} \\\ & \Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=\dfrac{50-49}{5} \\\ & \Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=\dfrac{1}{5} \\\ & \Rightarrow {{\left( x-\left( -1 \right) \right)}^{2}}+{{\left( y-3 \right)}^{2}}={{\left( \dfrac{1}{\sqrt{5}} \right)}^{2}} \\\ \end{aligned}
Now it is in the required form.
Comparing the above equation with the general equation of circle, we get
h=−1-1, k=3 and r=15\dfrac{1}{\sqrt{5}}
Hence, the center of the given circle is (−1-1, 3) and radius is 15\dfrac{1}{\sqrt{5}}.

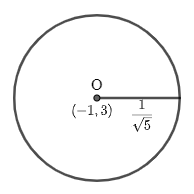
This is the required solution of the given question.

Note: The coefficient of ‘x2{{x}^{2}}’ and ‘y2{{y}^{2}}’ should be 1. So dividing the whole equation by ‘5’ should be the first approach for solving this question. In the general equation of circle (x−h)2+(y−k)2=(r)2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}} ‘h’ is the ‘x’- offset from the origin and ‘y’ is the ‘y’- offset from the origin.