Question

How do you find the axis of symmetry and the maximum or minimum value of the function $y={{x}^{2}}+3x$?

Answer 1

For this problem we need to find the axis of symmetry and the maximum or minimum value of the given function. We can observe that the given equation is a parabola. For parabolas we will decide whether it has maximum or minimum by observing the sign of the ${{x}^{2}}$ coefficient. So for the given equation we will check the sign of the ${{x}^{2}}$ coefficient and write if it has a maximum or minimum value. For parabolas $y=a{{x}^{2}}+bx+c$ we know that the minimum or maximum value is $-\dfrac{b}{2a}$. So, we will compare the given equation with the standard equation $y=a{{x}^{2}}+bx+c$ and calculate the required value.

Complete step by step answer:
Given equation $y={{x}^{2}}+3x$.
We can observe that the coefficient of the ${{x}^{2}}$ is $+1$. So, the given equation has a minimum value.
Comparing the given equation with the standard equation of parabola $y=a{{x}^{2}}+bx+c$, then we will get
$a=1$, $b=3$, $c=0$.
Now the minimum value of the given equation is
$\Rightarrow {{x}_{\min }}=-\dfrac{b}{2a}$
Substituting the values $b=3$, $a=1$ in the above equation, then we will get
$\begin{aligned} & \Rightarrow {{x}_{\min }}=-\dfrac{3}{2\left( 1 \right)} \\\ & \Rightarrow {{x}_{\min }}=-\dfrac{3}{2} \\\ \end{aligned}$
Now the ${{y}_{\min }}$ of the given equation can be calculated by substituting ${{x}_{\min }}$ in the given equation, then we will get
$\begin{aligned} & \Rightarrow {{y}_{\min }}=x_{\min }^{2}+3{{x}_{\min }} \\\ & \Rightarrow {{y}_{\min }}={{\left( -\dfrac{3}{2} \right)}^{2}}+3\left( -\dfrac{3}{2} \right) \\\ & \Rightarrow {{y}_{\min }}=\dfrac{9}{4}-\dfrac{9}{2} \\\ & \Rightarrow {{y}_{\min }}=-\dfrac{9}{4} \\\ \end{aligned}$
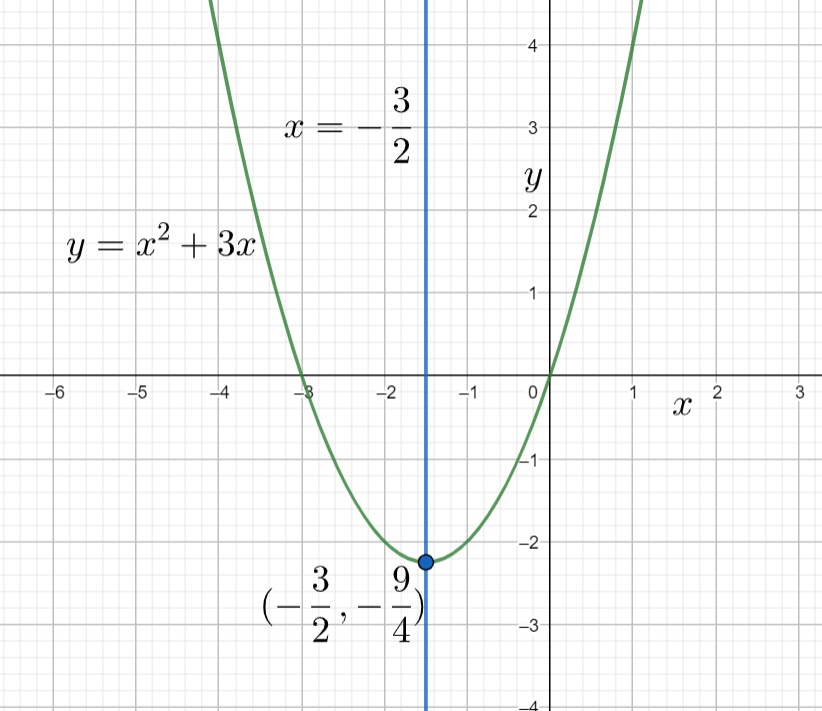
Hence the minimum value of the given equation is $\left( {{x}_{\min }},{{y}_{\min }} \right)=\left( -\dfrac{3}{2},-\dfrac{9}{4} \right)$.
Now the axis of symmetry for the given equation is ${{x}_{\min }}=-\dfrac{3}{2}$ or $x=-\dfrac{3}{2}$.
The diagram of the given equation with the calculated values is given by

Note: In this problem we have the coefficient of ${{x}^{2}}$ as positive and we have calculated the minimum value. If we have the coefficient of the ${{x}^{2}}$ then we will calculate the maximum value of the equation by using the same formula and the same procedure.