Question

How do you find the asymptotes for $y = \dfrac{{x + 2}}{{x + 3}}$ ?

Answer 1

First we will start by defining the asymptote, properties of asymptote and types of asymptote. Then we apply different conditions to evaluate the value of $x,y$.

Complete step by step answer:
We will first start by defining the asymptotes.
So, an asymptote is a straight line that continually approaches a given curve but does not meet it at any finite distance. There are three types of asymptotes namely: vertical asymptote, horizontal asymptote and oblique asymptote.
Vertical asymptotes occur as a denominator of a rational function tends to zero. Now, to find the equation equate the denominator to zero.
Hence, we substitute $x + 3$ equals to zero.
$x + 3 = 0 \\\ \,\,\,\,\,\,\,\,x = - 3 \\\$
Also, if the degree of the numerator and denominator are equal, as in our case both the degrees are $1$. The equation can be found by taking the ratio of leading coefficients.
$y = \dfrac{1}{1} \\\ y = 1 \\\$
Now plot the graph for asymptotes.

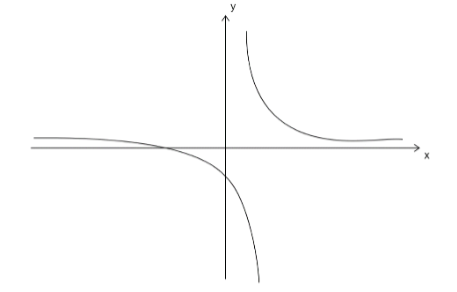
Additional Information: An asymptote is a line that a curve approaches, as it heads towards infinity.
The distance between the curve and the asymptote tends to zero as they head to infinity.
There are a total three types of asymptotes: horizontal, vertical and oblique asymptotes.**

Note: Always be sure that all of the terms are of the same type while equating them to zero. While defining types of asymptotes try to define them along with their respective properties. While plotting the graph always draw the axes first and then mark points and then plot the graph.