Solveeit Logo
Login

Question

Question: How do you find the area under the graph of \(f\left( x \right)=\cos \left( x \right)\) on the inter...

How do you find the area under the graph of f(x)=cos⁡(x)f\left( x \right)=\cos \left( x \right) on the interval [−π2,π2]\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right] ?

Explanation

Solution

To find the solution of the problem, we are to use the properties of integration. We need to transform this problem into an integration problem with limits according to the interval. Then integrating and using the trigonometric table identities, we will get the solution of the problem.

Complete step by step answer:
According to the question, we are to find the area of f(x)=cos⁡(x)f\left( x \right)=\cos \left( x \right)on the interval [−π2,π2]\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right].
So, to find the area, we are to use the properties of integration and transform it as an integration problem.
The following figure represents the given situation diagrammatically.

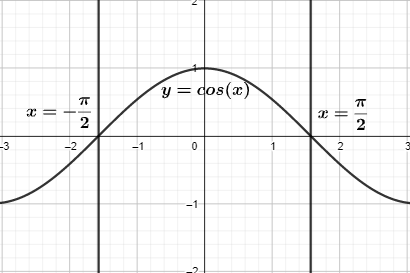
We will try to find the area under the area cos⁡(x)\cos \left( x \right)over the interval [−π2,π2]\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]. The period is closed and also inclusive because of the square brackets.
On the unit circle remember that the positive side of the y-axis corresponds to π2\dfrac{\pi }{2} and a coordinate of (0, 1). The y-coordinate corresponds to 1. On the unit circle remember that the negative side of the y-axis corresponds to −π2-\dfrac{\pi }{2} and a coordinate of (0, −1). The y-coordinate corresponds to −1.
Now, to find the integration, we will integrate cos x in the given range π2\dfrac{\pi }{2}and −π2-\dfrac{\pi }{2}.
Let us integrate, ∫−π2π2cos⁡x\int_{-\dfrac{\pi }{2}}^{\dfrac{\pi }{2}}{\cos x} .
Again, we have, ddx(sin⁡x)=cos⁡x\dfrac{d}{dx}\left( \sin x \right)=\cos x .
Thus, we get, ∫cos⁡x=sin⁡x\int{\cos x=\sin x}.
Using the limits, ∫−π2π2cos⁡x=[sin⁡x]−π2π2\int_{-\dfrac{\pi }{2}}^{\dfrac{\pi }{2}}{\cos x}=\left[ \sin x \right]_{-\dfrac{\pi }{2}}^{\dfrac{\pi }{2}}
Putting the values, [sin⁡(π2)−sin⁡(−π2)]\left[ \sin \left( \dfrac{\pi }{2} \right)-\sin \left( -\dfrac{\pi }{2} \right) \right]
Again, using the trigonometric table identities, sin⁡(π2)=1\sin \left( \dfrac{\pi }{2} \right)=1 and sin⁡(−π2)=−sin⁡(π2)=−1\sin \left( -\dfrac{\pi }{2} \right)=-\sin \left( \dfrac{\pi }{2} \right)=-1.
So, we have the value of the integration as, ∫−π2π2cos⁡x=1−(−1)=1+1=2\int_{-\dfrac{\pi }{2}}^{\dfrac{\pi }{2}}{\cos x}=1-\left( -1 \right)=1+1=2.
Thus, the area of the graph under the given interval is 2 units.

Note:
The area under a curve between two points can be found by doing a definite integral between the two points. To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b. Areas under the x-axis will come out negative and areas above the x-axis will be positive.