Question

How do you find the area of triangle ABC, given a=10, B=95, and c=35?

Answer 1

This type of question is based on the concept of the area of a triangle. We can solve this question with the help of the area of a triangle, that is, $Area=\dfrac{1}{2}ac\sin B$ , where B is the $\angle ABC$ . This formula is normally used to find the area of the triangle where two sides and an angle are given. Here, a=10, B= and c=35. We can find the value of $\sin B$ individually. Then, substitute $\sin B$ in the formula of area of the triangle.

Complete step by step answer:
It is given in the question that the triangle ABC has length a=10, $B={{95}^{\circ }}$ and c=35, that is AB=c=35 and BC=a=10 and $\angle ABC={{95}^{\circ }}$. And we have been asked to find the area of ABC.

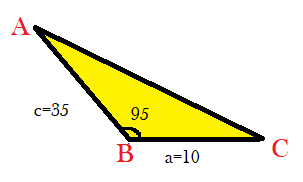
First, we have to find $\sin B$
Therefore,
$\sin B=\sin {{95}^{\circ }}$
We know that, $\sin {{95}^{\circ }}=0.9962$ (approximately).
$\therefore \sin B=0.9962$
Therefore, the area of the triangle ABC is
$Area=\dfrac{1}{2}ac\sin B$
We know that,
a=10,
c=35 and
$\sin B$=0.9962.
We get,
$Area=\dfrac{1}{2}\left( 10 \right)\left( 35 \right)\left( 0.9962 \right)$.
On further simplification, we get,
$Area=5\left( 35 \right)\left( 0.9962 \right)$
$Area=174.3$
Since, the unit of area is sq. units.
Hence, the area of the given triangle ABC is 174.3 sq. Units.

Note: Whenever we get this type of problem, we need to make sure about the formula used for the area of the triangle. Heron’s formula cannot be used to solve this type of question. Also, we should avoid calculation mistakes to obtain accurate answers.
The value of sin should be approximately calculated and should be rounded up to 4 decimal places to obtain an accurate solution.