Question

How do you find the area of the region bounded by the given curves? $y=\dfrac{1}{x},y={{x}^{2}},y=0,x=e$.

Answer 1

We have to find the area enclosed by these given equations. We will have to find the points of intersection of these given equations. The equations will then be integrated using the points of intersection as the intervals of the respective equation. And we proceed with the calculation to find the area of the region enclosed.

Complete step by step solution:
According to the given question, we have been given a set of equations and we have to find the area of the region that is bounded by these equations.
So, firstly we have to find the points of intersection of these equations, using which we will proceed on to find the area of the bounded region.
We will have to make a rough diagram of which equation intersects which and accordingly by the use of substitution method, we will find the points of intersection.
We will take $y=\dfrac{1}{x}$ and $y={{x}^{2}}$, the point of intersection can be found by substituting one equation into another.
We get,
$\Rightarrow {{x}^{2}}=\dfrac{1}{x}$
$\Rightarrow x=1$
We will find the value of ‘y’, we get,
$\Rightarrow y=\dfrac{1}{x}=1$
The point of intersection is $(1,1)$.
Now, between the equations $y=\dfrac{1}{x}$ and $x=e$, the point of intersection is,
The value of y-coordinate when $x=e$, we get,
$\Rightarrow y=\dfrac{1}{x}=\dfrac{1}{e}$
The point of intersection is $(e,\dfrac{1}{e})$.
$x=e$ is a line parallel to y - axis.
$y=0$ is nothing but the x – axis itself

The graph of the equations and points of intersection is given as below.

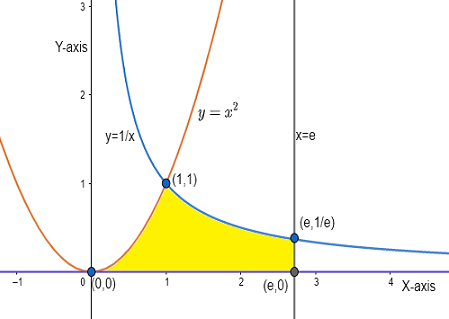
The points of intersection we found, will be used for intervals while integrating those equations and then we will get the area of the region bounded.
Area = integration of the eq. $y={{x}^{2}}$ + Integration of the eq. $y=\dfrac{1}{x}$
$Area=\int\limits_{0}^{1}{{{x}^{2}}dx}+\int\limits_{1}^{e}{\dfrac{1}{x}dx}$
We know that, $\int{{{x}^{n}}dx=}\dfrac{{{x}^{n+1}}}{n+1}$ and $\int{\dfrac{1}{x}dx=\ln x}$. We will be using these formulae to solve the above expression. We get,
$Area=\left[ \dfrac{{{x}^{3}}}{3} \right]_{0}^{1}+\left[ \ln x \right]_{1}^{e}$
Applying the intervals, we get,
$Area=\dfrac{1}{3}\left[ {{1}^{3}}-0 \right]+\left[ \ln e-\ln 1 \right]$
$Area=\dfrac{1}{3}+\ln e$ sq. units
Therefore, the area of the bounded region is $\dfrac{1}{3}+\ln e$.

Note: A rough diagram of the given equation should be drawn before starting to the solve for the area of the bounded region, in order to have clear picture of which equation intersects the other. Then, based on the intersection points we get our limits for those equations under consideration, therefore must be done step wise. Integration formulae and the expression must be written correctly to avoid any errors.