Question
Question: How do you find the area of the rectangle with vertices \[A(-5,1),B(-3,-1),C(3,5),D(1,7)\]?...
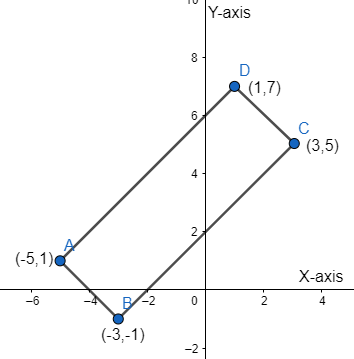
How do you find the area of the rectangle with vertices A(−5,1),B(−3,−1),C(3,5),D(1,7)?
Solution
We are given with the coordinates of the vertices of a rectangle. Firstly, we will find the length of the sides of the rectangle using the distance formula. Then, we will substitute the length of the sides of the rectangle in the formula for the area of the rectangle. On proceeding with solving the obtained expression, we will have the area of the rectangle.
Complete step by step solution:
According to the given question, we are provided with the coordinates of the vertices of the rectangle. We have to find the area of the rectangle.
We will begin by finding the lengths of sides of the rectangle and for that we will be using the distance formula.
Distance =(x2−x1)2+(y2−y1)2
So, the length of AB with coordinates A(−5,1),B(−3,−1)
=(−3−(−5))2+(−1−1)2
=(2)2+(−2)2
=4+4
=22units
Length of BC with coordinatesB(−3,−1),C(3,5)
=(3−(−3))2+(5−(−1))2
=(6)2+(6)2
=36+36
=62units
Length of CD with coordinates C(3,5),D(1,7)
=(1−3)2+(7−5)2
=(−2)2+(2)2
=4+4
=22units
Length of AD with coordinates A(−5,1),D(1,7)
=(1−(−5))2+(7−1)2
=(36)2+(36)2
=72
=62units
So, we obtained the lengths of all four sides of the rectangle. And we know that opposite sides of the rectangle are equal in length. So, length of the rectangle is 62 units and the breadth is 22 units.
As we know,
Area of the rectangle = Length of the rectangle × Breadth of the rectangle
=62×22
=6×2×2
=24 sq. units
Therefore, the area of the rectangle is 24 sq. units.
We have the graph of the given coordinates as follows:
Note: A rectangle is a 2D figure with length and breadth. Area of this rectangle is the product of length and breadth. When height is introduced in a rectangle then it becomes a cuboid which is a 3D figure. In the above solution, we used distance formula to measure the length of the sides of the rectangle, but we can also use it to prove that the given coordinates are the coordinates of vertices of a rectangle.
