Question
Question: How do you find the area of the equilateral triangle inscribed in a circle?...
How do you find the area of the equilateral triangle inscribed in a circle?
Solution
Hint : We will consider a circle with a radius r and an equilateral triangle inscribed in it. We are going to use the sine rule to get the area of the triangle. Area of the triangle is the half of the product of base and height, so with the help of the rule we will obtain the value of base and height. Then the area of the triangle.
Complete step-by-step answer :
First let’s draw the given scenario,
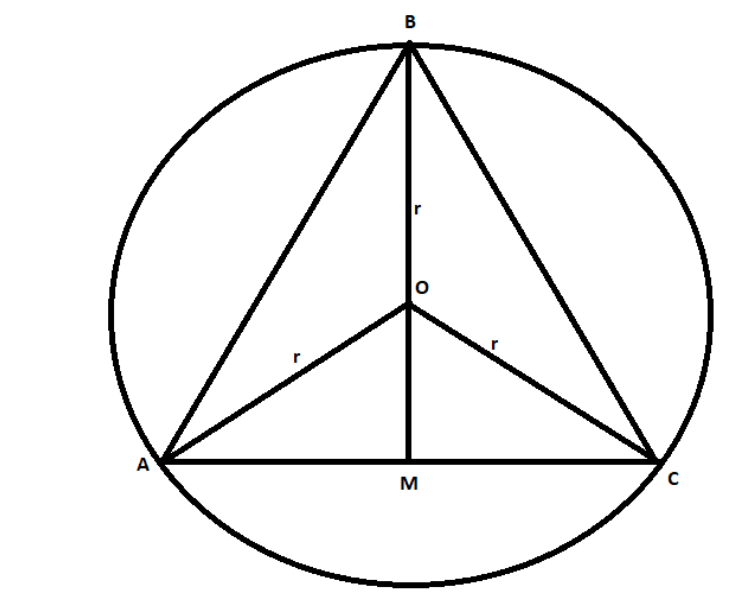
This is the overall situation. Now we know that △ABC is inscribed in the circle with radius r and center O. also that the given triangle is equilateral that has all angles measuring 60∘.
Now the formula to calculate the area of the triangle is,
area△=21×base×height
Now in the triangle above we will take AC as the base and BM as the height of the triangle. But we need to find the dimensions of the base and height.
For that we will take the help of sine rule that relates the lengths of the sides of the triangle with the sines of the angles opposite to the side. That is in the above case;
sin60∘AC=sin30∘OA
So the value of AC is,
AC=OAsin30∘sin60∘
Now we know that,
sin60∘=23&sin30∘=21
So substituting these values we get,
AC=OA2123
On calculating further,
AC=OA3
AC=r3 this is the value of base in the above case.
Now we need to find the value of BM.
We can observe from the figure above that, BM=BO+OM
Here BO is clearly visible as r but for OM;
In △OAM,
sin30∘=HypotenuseOpposite=rOM
So the value of OM is,
OM=r.sin30∘
Now putting both the values in the equation of BM,
BM=r+r.sin30∘
BM=r+2r
Taking the LCM,
BM=23r
Now using the formula of area;
A(△ABC)=21×(3r)×23r
On calculating we get,
A(△ABC)=433r2
This is the answer.
So, the correct answer is “A(△ABC)=433r2”.
Note : Note that use of sine formula is the way to get the dimensions of the base and height. We use the sin formula since it is a case of a triangle and the triangle is an equilateral triangle. But it is applicable to any other triangle also.
If a, b and c are the three sides of the △ABC
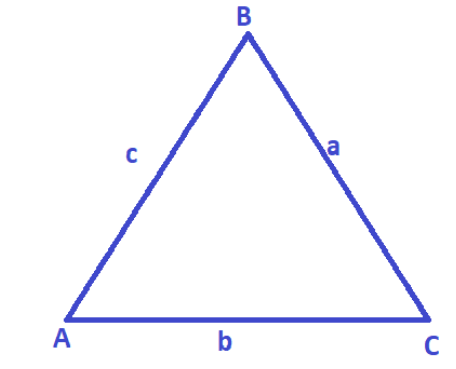
then we can say that sinAa=sinBb=sinCc
