Question

How do you find the area of one petal of $r = 2\cos (3\theta )$ ?

Answer 1

Hint : Here in this we have to find the area of one petal of $r = 2\cos (3\theta )$ . To find the area we use formula $A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r(\theta ))}^2}d\theta }$ , where $\alpha$ and $\beta$ are the limit points. Hence by substituting all the values in the formula and then by simplifying we obtain the area of one petal.

Complete step-by-step answer :
In general let us consider $r = a\sin (n\theta )$ or $r = a\sin (n\theta )$ where $a \ne 0$ and n is a positive number greater than 1. For the graph of rose if the value of n is odd then rose will have n petals or if the value of n is even then the rose will have 2n petals. Here “a” represents the radius of the circle where the rose petals lie.
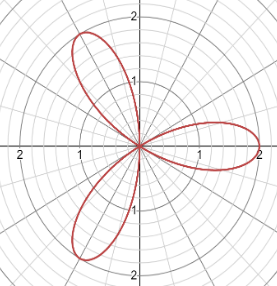
Now consider the given equation $r = 2\cos (3\theta )$ . Here a=2, the radius of the circle is 2 and n=3, the number is odd so we have 3 petals for the rose.
The figure is as shown

To find the area we use the formula $A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r(\theta ))}^2}d\theta }$ ------- (1)
Here the limits points are not given. Therefore, we have to find the value of $\alpha$ and $\beta$
Now consider the given equation $r = 2\cos (3\theta )$ ------- (2)
Substitute r=0 in equation (2) we have
$\Rightarrow 0 = 2\cos (3\theta )$
This is written as
$\Rightarrow 0 = \cos (3\theta )$
By taking the inverse we have
$\Rightarrow {\cos ^{ - 1}}(0) = 3\theta$
By the table of trigonometry ratios for standard angles in radians we have $\cos \left( {\dfrac{\pi }{2}} \right) = 1$ so we have
$\Rightarrow \dfrac{\pi }{2} = 3\theta$
Dividing by 3 on the both sides we have
$\Rightarrow \theta = \dfrac{\pi }{6}$
Therefore $\left( {\alpha ,\beta } \right) = \left( {r,\theta } \right) = \left( {0,\dfrac{\pi }{6}} \right)$ ----------- (3)
Substituting equation (2) and equation (3) in equation (1) we have
$A = 2 \times \dfrac{1}{2}\int_0^{\dfrac{\pi }{6}} {{{(2\cos (3\theta ))}^2}d\theta }$
Applying square, we have
$\Rightarrow A = 2 \times \dfrac{1}{2}\int_0^{\dfrac{\pi }{6}} {\left( {4{{\cos }^2}(3\theta )} \right)d\theta }$
On simplifying we have
$\Rightarrow A = 4\int_0^{\dfrac{\pi }{6}} {\left( {{{\cos }^2}(3\theta )} \right)d\theta }$
Apply the half angle formula for the cosine function we have
$\Rightarrow A = 4\int_0^{\dfrac{\pi }{6}} {\left( {\dfrac{{1 + \cos (6\theta )}}{2}} \right)d\theta }$
On simplifying we have
$\Rightarrow A = 4 \times \dfrac{1}{2}\int_0^{\dfrac{\pi }{6}} {\left( {1 + \cos (6\theta )} \right)d\theta }$
Take integral to each term we have
$\Rightarrow A = 2\left( {\int_0^{\dfrac{\pi }{6}} {d\theta } + \int_0^{\dfrac{\pi }{6}} {\cos (6\theta )d\theta } } \right)$
On applying the integration, we have
$\Rightarrow A = 2\mathop {[\theta ] }\nolimits_0^{\dfrac{\pi }{6}} + 2\left[ {\dfrac{{\sin (6\theta )}}{6}} \right] _0^{\dfrac{\pi }{6}}$
Applying the limit points, we get
$\Rightarrow A = 2\left[ {\dfrac{\pi }{6} - 0} \right] + \dfrac{2}{6}\left[ {\sin 6\left( {\dfrac{\pi }{6}} \right) - \sin (0)} \right]$
On simplifying we get

$$\Rightarrow A = \dfrac{\pi }{3} + \dfrac{1}{3}\left[ {0 - 0} \right] \\\ \Rightarrow A = \dfrac{\pi }{3}sq.units \;$$

Therefore, the area of one petal of $r = 2\cos (3\theta )$ is $\dfrac{\pi }{3}\;sq.units$
So, the correct answer is “ $\dfrac{\pi }{3}\;sq.units$ ”.

Note : The area of a petal for the circle for the polar coordinates is given by $A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r(\theta ))}^2}d\theta }$ . The unit for the area is given as a square unit. In the polar form the coordinates are represented in the form of $\left( {r,\theta } \right)$ where r represents the radius of the circle and the $\theta$ represents the angle.