Question

How do you find the area of a triangle whose vertices are $A(2,4)$, $B( - 2,0)$ and $C(4, - 2)$.

Answer 1

We use the concepts of geometry, triangle and matrices to solve this problem. A triangle is a polygon (a closed figure) of three sides. A matrix is a group of elements arranged in different numbers of rows and columns. It is represented as ${A_{m \times n}}$ where $m$ is the number of rows and $n$ is the number of columns.

Complete step by step solution:
The triangle formed by points $A(2,4)$, $B( - 2,0)$ and $C(4, - 2)$ is given below.

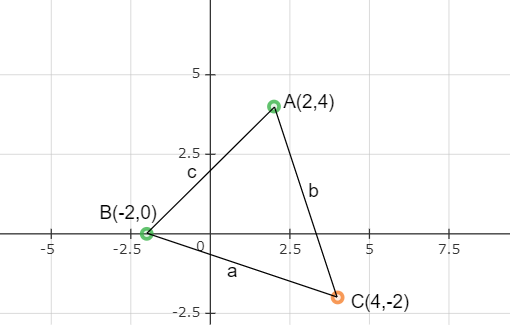
The side opposite to point ‘A’ is $a$ units.
The side opposite to point ‘B’ is $b$ units.
The side opposite to point ‘C’ is $c$ units.
Area of a triangle with vertices $\left( {{x_1},{y_1}} \right)$, $\left( {{x_2},{y_2}} \right)$ and $\left( {{x_3},{y_3}} \right)$ is given by half times the determinant of matrix ‘A’, where A = \left( {\begin{array}{*{20}{c}} {{x_1}}&{{y_1}}&1 \\\ {{x_2}}&{{y_2}}&1 \\\ {{x_3}}&{{y_3}}&1 \end{array}} \right)
So, mathematically, $Area = \dfrac{1}{2}|A|$ square units.
So, area of this triangle is

{{x_1}}&{{y_1}}&1 \\\ {{x_2}}&{{y_2}}&1 \\\ {{x_3}}&{{y_3}}&1 \end{array}} \right| = \left| {\begin{array}{*{20}{c}} 2&4&1 \\\ { - 2}&0&1 \\\ 4&{ - 2}&1 \end{array}} \right|$$ We all know that, determinant of a matrix $$\left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}} \\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}} \\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right)$$ is equal to $$\det = {a_{11}}({a_{22}}{a_{33}} - {a_{32}}{a_{23}}) - {a_{12}}({a_{21}}{a_{33}} - {a_{31}}{a_{23}}) + {a_{13}}({a_{21}}{a_{32}} - {a_{31}}{a_{22}})$$ So, we get, $$Area = \dfrac{1}{2}.\left( {2((0)1 - ( - 2)1) - 4(( - 2)1 - (4)1) + 1(( - 2)( - 2) - (4).0)} \right)$$ $$ \Rightarrow Area = \dfrac{1}{2}.\left( {2(0 + 2) - 4( - 2 - 4) + 1(4 - 0)} \right)$$ On further simplification, we get finally, $$ \Rightarrow Area = \dfrac{1}{2}.\left( {4 + 24 + 4} \right) = \dfrac{1}{2}\left( {32} \right) = 16$$ **Therefore, we can conclude that, the area of a triangle with vertices $$A(2,4)$$, $$B( - 2,0)$$ and $$C(4, - 2)$$ is equal to 16 square units.** **Note:** We can also find the area of a triangle in another way. Let the lengths of sides of a triangle be $$a,b,c$$. Then area is given by $$area = \sqrt {s(s - a)(s - b)(s - c)} $$, where $$s = \dfrac{{a + b + c}}{2}$$. Length of a line joining the points $$\left( {{x_1},{y_1}} \right)$$ and $$\left( {{x_2},{y_2}} \right)$$ is given by $$\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $$. Determinant of a matrix is defined as the sum of product of an element and its cofactor matrix in any row or a column. Cofactor matrix is defined as $${C_{ij}} = {( - 1)^{i + j}}|{M_{ij}}|$$, where $${M_{ij}}$$ is a minor element. A minor of an element is gained by removing the row and the column containing that element.