Question

How do you find the area of a triangle bounded by the y axis, the line $f\left( x \right) = 7 - \dfrac{4}{5}x$, and the line perpendicular to $f\left( x \right)$ that passes through the origin?

Answer 1

The given function is of the form, $y = mx + c$, in which we have slope from the given function, hence to find the area of triangle bounded by y axis we need to find Slope of perpendicular line then find the points using equation of perpendicular line passing through origin, and next we need to find the area of a triangle by substituting the obtained points in the formula: ${A_t} = \dfrac{1}{2} \cdot y \cdot x$.

Formula used:
${A_t} = \dfrac{1}{2} \cdot y \cdot x$
${A_t}$ is Area of the triangle.
x and y are the points of the triangle.
${m_p} = - \dfrac{1}{m}$
${m_p}$ is Slope of the perpendicular line.
$m$ is the slope of a line.

Complete step by step solution:
Given,
$f\left( x \right) = 7 - \dfrac{4}{5}x$,
The given function is of the form, $y = mx + c$, in which we have slope from the given function i.e.,
$f\left( x \right) = y = 7 - \dfrac{4}{5}x$;
Slope is $m = - \dfrac{4}{5}$.
Slope of perpendicular line is: ${m_p} = - \dfrac{1}{m}$
$\Rightarrow {m_p} = - \dfrac{1}{{ - \dfrac{4}{5}}}$
$\Rightarrow {m_p} = \dfrac{5}{4}$
Equation of perpendicular line passing through origin is $y = \dfrac{5}{4}x$, intersecting point between the lines is:
$\dfrac{5}{4}x = 7 - \dfrac{4}{5}x$
We, need to combine and simplify the x terms as:
$\Rightarrow \dfrac{5}{4}x + \dfrac{4}{5}x = 7$
Hence, to simplify we have lcm as 20, hence we get:
$\Rightarrow \dfrac{{\left( {5 \times 5} \right) + \left( {4 \times 4} \right)}}{{20}}x = 7$
$\Rightarrow \dfrac{{25 + 16}}{{20}}x = 7$
Evaluate the terms, as:
$\Rightarrow \dfrac{{41}}{{20}}x = 7$
$\Rightarrow 41x = 7\left( {20} \right)$
$\Rightarrow 41x = 140$
To find, the value of x, shift the terms to evaluate as:
$\Rightarrow x = \dfrac{{140}}{{41}}$
As, we have equation of perpendicular line passing through origin is $y = \dfrac{5}{4}x$, hence substitute the value of x in this equation as:
$y = \dfrac{5}{4}x$
$\Rightarrow y = \dfrac{5}{4} \cdot \dfrac{{140}}{{41}}$
Multiply the terms, as:
$\Rightarrow y = \dfrac{{5 \times 140}}{{4 \times 41}} = \dfrac{{700}}{{164}}$
Hence, we get:
$\Rightarrow y = \dfrac{{175}}{{41}}$
Therefore, we have: $x = \dfrac{{140}}{{41}}$ and $y = \dfrac{{175}}{{41}}$.
Hence, y-intercept of line is:
$y = 7 - \dfrac{4}{5}x$; $y = 7$,
Hence, the triangle is bounded by the points x, y is $\left( {0,0} \right),\left( {0,7} \right)$and $\left( {\dfrac{{140}}{{41}},\dfrac{{175}}{{41}}} \right)$.

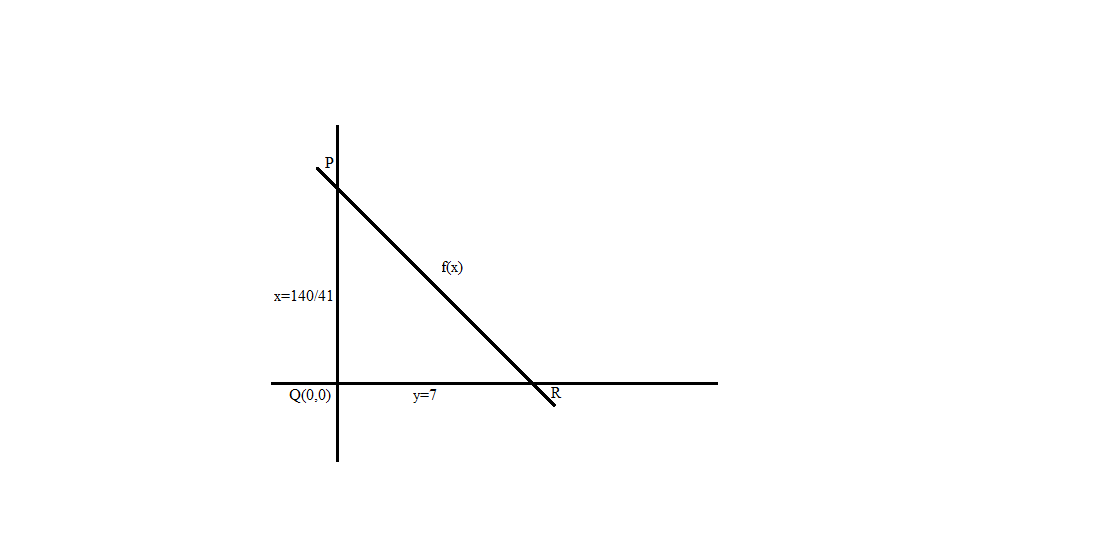
In the figure, PQR is a triangle bounded by the y axis, the line $f\left( x \right) = 7 - \dfrac{4}{5}x$, and the
Area of the triangle is:
$\Rightarrow {A_t} = \dfrac{1}{2} \cdot y \cdot x$
$\Rightarrow {A_t} = \dfrac{1}{2} \cdot 7 \cdot \dfrac{{140}}{{41}}$
Multiply the terms, as:
$\Rightarrow {A_t} = \dfrac{{1 \times 7 \times 140}}{{2 \times 41}} = \dfrac{{980}}{{82}}$
$\Rightarrow {A_t} = \dfrac{{490}}{{41}} \approx 11.95$
Therefore, Area of the triangle is 11.95 sq. units.

Note: The key point to solve the given function i.e., to find area of triangle, we must know what type of function is given for ex: point slope form, slope intercept form etc, hence based on this we need to apply formulas and simplify the terms in Equation of perpendicular line to get the points and then find the area of triangle.