Question

How do you find the area of a trapezoid with vertices $(-7,1),(-4,4),(-4,-6),(-7,-3)$?

Answer 1

We are given with the vertices of a trapezoid whose area we have to find. We will first graph the points given to us. Then we will measure the length of the parallel sides and also the height between the parallel sides. Then, we will use the formula of the area of trapezoid, which is, $\dfrac{1}{2}({{b}_{1}}+{{b}_{2}})h$. Hence, we have the area of the trapezoid.

Complete step by step solution:
According to the given question, we are given vertices of a trapezoid and using that we have to find the area of the trapezoid.
So at first, we will graph the given coordinates. And we get a trapezoid.
Now, we will calculate the length of the parallel sides which we will then put in the formula for area of trapezoid.
We know that distance between the two coordinates $({{x}_{1}},{{y}_{1}})$ and $({{x}_{2}},{{y}_{2}})$ can be given by:
Distance $=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$
So, we have the graph of the coordinates given to us below.

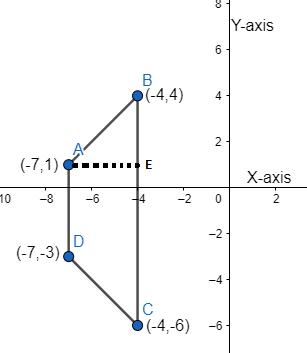
We can see that $AD||BC$, so we have to find the lengths of AD and BC.
Length of AD $=\sqrt{{{(-3-1)}^{2}}+{{(-7-(-7))}^{2}}}$
$=\sqrt{{{(-4)}^{2}}+{{(-7+7)}^{2}}}$
$=\sqrt{16+0}$
$=4units$
Length of BC $=\sqrt{{{(-6-4)}^{2}}+{{(-4-(-4))}^{2}}}$
$=\sqrt{{{(-10)}^{2}}+{{(-4+4)}^{2}}}$
$=\sqrt{100+0}$
$=10units$
Now, we have to find the distance between the two parallel lines, that is, the distance between the lines AD and BC.
For that we will just subtract the values of X-coordinate in the two lines.
X-coordinate of the line AD is -7 and of the line BC is -4.
The distance AE $=-4-(-7)$
$=-4+7$
$=3units$
Now, we have all the values we require, so we will substitute these values in the area of trapezoid and we get,
$Area=\dfrac{1}{2}({{b}_{AD}}+{{b}_{BC}})h$
$\Rightarrow Area=\dfrac{1}{2}(4+10)\times 3$
$\Rightarrow Area=\dfrac{1}{2}(14)\times 3$
$\Rightarrow Area=7\times 3=21$ sq. units
Therefore, the area of the trapezoid is 21 sq. units

Note: Trapezoid figures are not the conventional figures that we usually deal with, so their figure, formula of area should be written carefully and correctly. Trapezoids only take into account the length of the parallel sides and the distance between them. The non-parallel sides are not of any importance in the area of trapezoid. So, before working on trapezoid figures, clearly picture out the parallel sides to make the calculations faster.