Question
Question: How do you find the area of a regular hexagon with a radius of \(5?\) Please show working....
How do you find the area of a regular hexagon with a radius of 5? Please show working.
Solution
Area of a regular hexagon with radius “r” is given by 2r2nsin(n3600) where “n” is the number of sides of the regular hexagon. Show working with the help of a figure and try to derive the above formula.
Complete step by step solution:
Do you know how the area of a regular hexagon is equals to
2r2nsin(n3600), let us derive this and see how it comes.
Draw a regular hexagon with side 2a and radius R Now in this regular hexagon, we can see from figure ΔABD, if we find the area of ΔABD and multiply it by 6 then we will get the required area of hexagon. Since, we know that in a regular hexagon two times its length of side (2a) is equals to its diameter (2R)
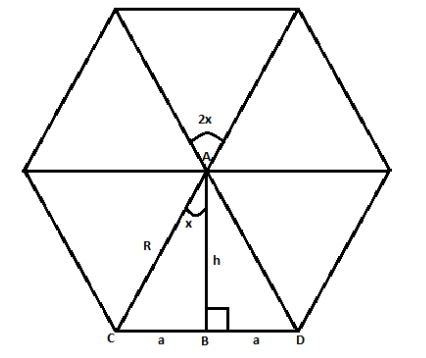
⇒2R=2×2a ⇒R=2a−−−−(i)
Now the area of the ΔABD can be written as
=21×base×heigth = 21×CD×AB = 21×2a×hFrom equation (i) we know that R=2a and in ΔABC we have
cosx=ACAB=Rh ⇒h=Rcosx
We can also write cosx=sin(900−x)
⇒h=Rsin(900−x)
Putting 2a=Randh=Rsin(900−x) in above area expression,
= 21×2a×h = 21×R×Rsin(900−x) = 21×R2sin(900−x)From figure, we can write $$6 \times 2x = {360^0} \Rightarrow x = \dfrac{{{{360}^0}}}{{12}}
\Rightarrow x = {30^0}$$ so the above expression will be
= 21×R2sin(900−x) = 21×R2sin(900−300) = 21×R2sin600So we get the area of ΔABD, now multiplying it by n=6 (number of triangles) to get area of the hexagon
=6×21×R2sin600
Now substituting the given value of radius, R=5 we will get
=6×21×R2sin600 =6×21×52sin600 =6×21×25×sin600 =75×sin600
We know the value of sin600=23
=75×sin600 =75×23 =64.952unit2
∴ the required area of regular hexagon with radius 5units = 64.952unit2
Note: Apart from regular and irregular hexagon, hexagon is also classified as concave and convex hexagon, concave hexagon has one or more interior angles >1800 whereas in convex hexagon none of its interior angles is >1800 and also the regular hexagon is always a convex one.
