Question

How do you find the area of a circle using integration?

Answer 1

We use the polar coordinate system and write the area of the circle using integration of the small part of the circle which forms a triangle. Use limits of integration for angles as 0 to $2\pi$and integrate the area of the small triangle to the complete angle $2\pi$.

• Area of a triangle is given by half of the base multiplied by its height.

Complete step-by-step answer:
Let us assume a circle having polar coordinates $(r,\theta )$
We draw the diagram for the circle where we draw the small part of the circle with a small angle and arc length such that it becomes a straight line.

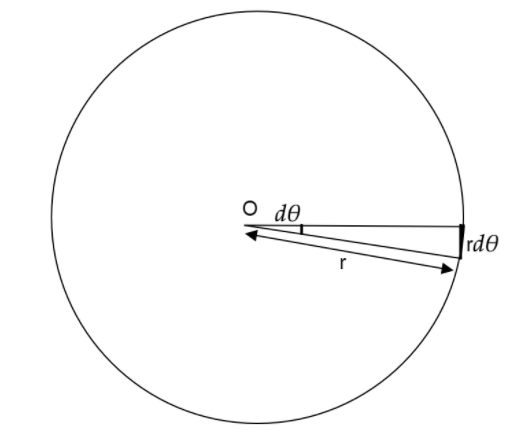
Then we take small part of the area which has radius $dr$and angle $d\theta$
Since arc length of drawn portion can be given by $rd\theta$, then the area of triangle formed will be given by $\dfrac{1}{2} \times$base $\times$height
$\Rightarrow$Area of the triangle $= \dfrac{1}{2} \times rd\theta \times r$
$\Rightarrow$Area of the triangle $= \dfrac{{{r^2}}}{2}d\theta$ … (1)
If we have to find the complete area of the circle then we will integrate the derivative of angle from 0 to $2\pi$, i.e. we integrate the area of triangle from the angle 0 to $2\pi$
$\Rightarrow$Area of the complete circle $= \int\limits_0^{2\pi } {\dfrac{{{r^2}}}{2}d\theta }$
Now we bring out constant value from the integral
$\Rightarrow$Area of circle $= \dfrac{{{r^2}}}{2}\int\limits_0^{2\pi } {d\theta }$
Now we integrate the angle from 0 to $2\pi$
$\Rightarrow$Area of circle $= \dfrac{{{r^2}}}{2}(2\pi )$
Cancel same factors from numerator and denominator
$\Rightarrow$Area of circle $= \pi {r^2}$

$\therefore$Area of circle is $\pi {r^2}$

Note:
Many students get confused between the polar coordinates as they are only aware about the equation of the circle in x-y coordinate. We have a polar form of coordinates where the coordinates are dependent on the angle and the radius of the circle. Also, when integrating the terms having double derivatives, always solve the integral inside the integral first and then apply the final integral to the calculated value.