Question

How do you find the area between $x = 4 - {y^2}$ and $x = y - 2$ ?

Answer 1

Hint : In order to find the area, we need to know the region between the equations, and from the equation we can see that the first equation would represent a parabola and the second one would represent a straight line. Compare the two equations to find the points of intersection then using integration find the area inside them.
Formula used:
$\int {{x^n}dx = \dfrac{{{x^{n + 1}}}}{{n + 1}}}$
$\int {adx = } a\int {dx}$

Complete step-by-step answer :
The first Equation given is: $x = 4 - {y^2}$ and the second is $x = y - 2$ .
Since, value of $x$ is given in both, so comparing the two equations, we get:
$4 - {y^2} = y - 2 \\\ {y^2} + y - 6 = 0 \;$
Comparing the obtained Quadratic Equation with the standard Quadratic Equation $a{x^2} + bx + c = 0$ , we get:
$a = 1 \\\ b = 1 \\\ c = - 6 \;$
Solving for discriminant, we get:
$D = \sqrt {{b^2} - 4ac} \\\ D = \sqrt {{1^2} - 4 \times 1 \times \left( { - 6} \right)} \\\ D = \sqrt {1 + 24} \\\ D = \sqrt {25} = 5 \;$
Quadratic Formula to find both roots of a quadratic equation as
$y_1 = \dfrac{{ - b + \sqrt {{b^2} - 4ac} }}{{2a}}$ and $y_2 = \dfrac{{ - b - \sqrt {{b^2} - 4ac} }}{{2a}}$
$y_1,y_2$ are root to quadratic equations $a{x^2} + bx + c$ .
For, $y_1$ :
$y_1 = \dfrac{{ - b + \sqrt {{b^2} - 4ac} }}{{2a}} \\\ y_1 = \dfrac{{ - 1 + 5}}{{2 \times 1}} = \dfrac{4}{2} = 2 \\\$
For, $y_2$ :
$y_2 = \dfrac{{ - b - \sqrt {{b^2} - 4ac} }}{{2a}} \\\ y_2 = \dfrac{{ - 1 - 5}}{{2 \times 1}} = \dfrac{{ - 6}}{2} = - 3 \;$
Hence the factors will be $(y - y_1)\,and\,(y - y_2)\,$ that is $(y - 2)\,and\,(y + 3)\,$ .
Putting the values of $y_1$ and $y_2$ in the equation $x = y - 2$ one by one to get $x_1$ and $x_2$ :
$x_1 = y_1 - 2 = 2 - 2 = 0$
$x_2 = y_2 - 2 = - 3 - 2 = - 5$
Therefore, the points of intersection are:
$(x_1,y_1)\,and\,(x_2,y_2)\,$ , which are $(0,2)\,and\,( - 5, - 3)\,$ .
According to the points obtained, the graph would be:

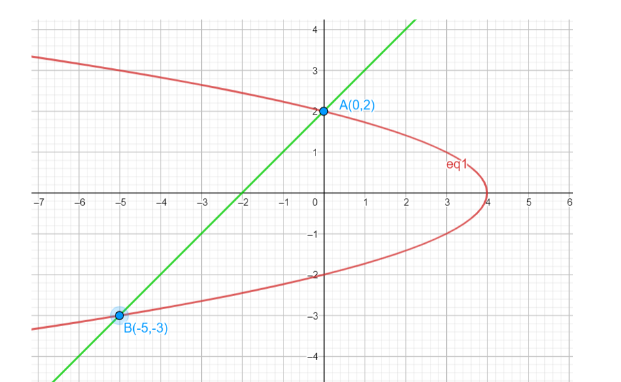
Since, the starting and ending points for the y-axis are: $- 3and2$ .So, the area is starting from $- 3to2$ .
Writing the first and second equation in terms of $y$ and we get:
$x = 4 - {y^2} = > y = \sqrt {4 - x}$
$x = y - 2 = > y = x + 2$
The area under the equation is:
$A = \int\limits_{ - 3}^2 {\left[ {\left( {4 - {y^2}} \right) - \left( {y - 2} \right)} \right]} dy$
On further solving, we get:
$A = \int\limits_{ - 3}^2 {\left[ {\left( {4 - {y^2}} \right) - \left( {y - 2} \right)} \right]} dy \\\ A = \int\limits_{ - 3}^2 {\left[ {4 - {y^2} - y + 2} \right]} dy \\\ A = \int\limits_{ - 3}^2 {\left[ { - {y^2} - y + 6} \right]} dy \\\ A = - \int\limits_{ - 3}^2 {{y^2}} dy - \int\limits_{ - 3}^2 y dy + 6\int\limits_{ - 3}^2 {dy} \\\ A = - {\left[ {\dfrac{{{y^3}}}{3}} \right]_{ - 3}}^2 - {\left[ {\dfrac{{{y^2}}}{2}} \right]^2}_{ - 3} + 6{\left[ y \right]^2}_{ - 3} \\\ A = - \left[ {\dfrac{{{2^3}}}{3} - \dfrac{{{{\left( { - 3} \right)}^3}}}{3}} \right] - \left[ {\dfrac{{{2^2}}}{2} - \dfrac{{{{\left( { - 3} \right)}^2}}}{2}} \right] + 6\left[ {2 - \left( { - 3} \right)} \right] \\\ A = - \left[ {\dfrac{8}{3} + 9} \right] - \left[ {2 - \dfrac{9}{2}} \right] + 6\left[ {2 + 3} \right] \\\ A = - \dfrac{8}{3} - 9 - 2 + \dfrac{9}{2} + 30 \\\ A = - \dfrac{8}{3} - 11 + \dfrac{9}{2} + 30 \\\ A = \dfrac{{125}}{6} = 20.833 \;$
Therefore, the area between $x = 4 - {y^2}$ and $x = y - 2$ is $20.833$ sq. units.
So, the correct answer is “ $20.833$ sq. units.”.

Note : It's important to find the intersecting points to know the area covered by the parabola and the straight line.
We can also take the value of $x$ instead of y to find the area, just the values inside the integration would be written in terms of $x$ and $dx$ .