Question

How do you find the area between the loop of $r = 1 + 2\cos \theta$?

Answer 1

Here in this we have to find the area between the loop of $r = 1 + 2\cos \theta$. To find the area we use formula $A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r)}^2}d\theta }$, where $\alpha$and $\beta$ are the limit points. Hence by substituting all the values in the formula and then by simplifying we obtain the area of one petal.

Complete step by step explanation:
In generally let we consider $r = a \pm b\sin (\theta )$ or $r = a \pm b\cos (\theta )$ where $a > 0$, $b > 0$ and $a \ne b$
Now consider the given equation $r = 1 + 2\cos \theta$. Here a=1, and b=2 , graph the limacon as shown

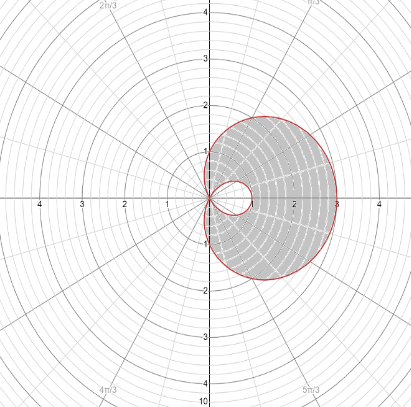
To find the area we use the formula
$A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r)}^2}d\theta }$------- (1)
Here the limits points are not given.
Therefore, we have to find the value of
$\alpha$ and $\beta$
Now consider the given equation
$r = 1 + 2\cos \theta$ ------- (2)
Substitute r=0 in equation (2) we have
$\Rightarrow 0 = 1 + 2\cos (\theta )$
This is written as
$\Rightarrow - \dfrac{1}{2} = \cos (\theta )$
By taking the inverse we have
$\Rightarrow {\cos ^{ - 1}}\left( { - \dfrac{1}{2}} \right) = \theta$
$\Rightarrow \theta = \dfrac{{2\pi }}{3}$ and $\theta = \dfrac{{4\pi }}{3}$.
Therefore $\theta$ varies from the angle $\dfrac{{2\pi }}{3}$ to angle $\dfrac{{4\pi }}{3}$

\right)$$----------- (3) Substituting equation (2) and equation (3) in equation (1) we have $$A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {{{(1 + 2\cos (\theta ))}^2}d\theta }

Applying the algebraic formula ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$
$\Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {(1 + 4\cos \left( \theta \right) + 4{{\cos }^2}(\theta ))d\theta }$
It can be also written as
$\Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {(1 + 4\cos \left( \theta \right) + 2.2{{\cos }^2}(\theta ))d\theta }$
Apply the double angle formula for the cosine function,$\cos 2x = 2{\cos ^2}x - 1\,\,\, \Rightarrow \,\,\,2{\cos ^2}x = \cos 2x + 1$, then
$\Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\left( {1 + 4\cos \left( \theta \right) + 2.\left( {\cos (2\theta ) + 1} \right)} \right)d\theta }$

\theta \right) + 2\cos (2\theta ) + 2} \right)d\theta } $$ On simplifying we have $$ \Rightarrow A = \dfrac{1}{2}\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\left( {3 + 4\cos \left( \theta \right) + 2\cos (2\theta )} \right)d\theta } $$ Take integral to each term we have $$ \Rightarrow A = \dfrac{1}{2}\left( {3\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {d\theta } + 4\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\cos \left( \theta \right)d\theta } + 2\int_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}} {\cos (2\theta )} d\theta } \right)$$ On applying the integration, we have $$ \Rightarrow A = \dfrac{1}{2}\left( {3\theta + 4\sin \left( \theta \right) + 2\dfrac{{\sin (2\theta)}}{2}} \right)_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}}$$ $$ \Rightarrow A = \dfrac{1}{2}\left( {3\theta + 4\sin \left( \theta \right) + \sin (2\theta )} \right)_{\dfrac{{2\pi }}{3}}^{\dfrac{{4\pi }}{3}}$$ Applying the limit points, we get $$ \Rightarrow A = \dfrac{1}{2}\left( {3 \cdot \dfrac{{4\pi }}{3} + 4\sin \left( {\dfrac{{4\pi }}{3}}\right) + \sin \left( {2 \cdot \dfrac{{4\pi }}{3}} \right) - 3 \cdot \dfrac{{2\pi }}{3} - 4\sin \left({\dfrac{{2\pi }}{3}} \right) + \sin \left( {2 \cdot \dfrac{{2\pi }}{3}} \right)} \right)$$ On simplifying we get $$ \Rightarrow A = \dfrac{1}{2}\left( {4\pi + 4\left( { - \dfrac{{\sqrt 3 }}{2}} \right) + \left( {\dfrac{{\sqrt 3 }}{2}} \right) - 2\pi - 4\left( {\dfrac{{\sqrt 3 }}{2}} \right) - \left( { - \dfrac{{\sqrt 3 }}{2}} \right)} \right)$$ $$ \Rightarrow A = \dfrac{1}{2}\left( {4\pi - \dfrac{{4\sqrt 3 }}{2} + \dfrac{{\sqrt 3 }}{2} - 2\pi - \dfrac{{4\sqrt 3 }}{2} + \dfrac{{\sqrt 3 }}{2}} \right)$$ $$ \Rightarrow A = \dfrac{1}{2}\left( {2\pi - 2 \cdot \dfrac{{4\sqrt 3 }}{2} + 2 \cdot \dfrac{{\sqrt 3 }}{2}} \right)$$ $$ \Rightarrow A = \dfrac{1}{2}\left( {2\pi - 4\sqrt 3 + \sqrt 3 } \right)$$ $$ \Rightarrow A = \dfrac{1}{2}\left( {2\pi - 3\sqrt 3 } \right)$$ $$ \Rightarrow A = \pi - \dfrac{{3\sqrt 3 }}{2}$$ **Therefore, the area between the loop of $$r = 1 + 2\cos \theta $$ is $$\therefore \,\,\,A = \pi - \dfrac{{3\sqrt 3 }}{2}$$** **Note:** The area of a petal for the circle for the polar coordinates is given by $$A = \dfrac{1}{2}\int_\alpha ^\beta {{{(r(\theta ))}^2}d\theta } $$. The unit for the area is given as square unit. In the polar form the coordinates are represented in the form of $$\left( {r,\theta } \right)$$where r represents the radius of the circle and the $$\theta $$represents the angle.